About
Topics
Measurement of length and timeDescription
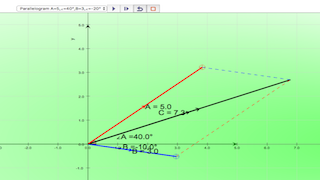
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. What if the customary x-y coordinate axes is not (horizontal) and (vertical)? Sometimes, it could be useful to resolve vectors along and perpendicular to a slope, direction of travel than always horizontal and vertical,What is shown here?
1. What are the x and y components of the RED vector A?2. record down on a piece of paper.
3. What are the x and y components of the BLUE vector B?.
4. record down on a piece of paper.
5. now, you have the values of (Ax, Ay) = _______ and (Bx, By) = _______
How to calculate the resultant of 2 vectors?
1. click PLAY to visualise the meaning of addition of vector A with B.2. What are the components of this vector sum?
3. How do they relate to the components of the original (RED and BLUE) vectors?
4. The vector (BLACK) sum C = (Cx, Cy) is now a vector that reaches from the tail of the first (RED) A = (Ax,Ay) vector to the head of the second (BLUE) B = (Bx,By) vector.
5. test yourself whether you have enough practice calculating C = (Cx,Cy).
Other interesting fun activities
1. this model can be used to calculate any A & B vectors.4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.sg/2014/10/vector-addition-model.html
Sample Learning Goals
(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of eachVersion:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Learning Design
London Knowledge Lab - Institute of Education
How to Use
Topics
Measurement of length and time
Description
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. What if the customary x-y coordinate axes is not (horizontal) and (vertical)? Sometimes, it could be useful to resolve vectors along and perpendicular to a slope, direction of travel than always horizontal and vertical,
What is shown here?
1. What are the x and y components of the RED vector A?
2. record down on a piece of paper.
3. What are the x and y components of the BLUE vector B?.
4. record down on a piece of paper.
5. now, you have the values of (Ax, Ay) = _______ and (Bx, By) = _______
How to calculate the resultant of 2 vectors?
1. click PLAY to visualise the meaning of addition of vector A with B.
2. What are the components of this vector sum?
3. How do they relate to the components of the original (RED and BLUE) vectors?
4. The vector (BLACK) sum C = (Cx, Cy) is now a vector that reaches from the tail of the first (RED) A = (Ax,Ay) vector to the head of the second (BLUE) B = (Bx,By) vector.
5. test yourself whether you have enough practice calculating C = (Cx,Cy).
Other interesting fun activities
1. this model can be used to calculate any A & B vectors.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.sg/2014/10/vector-addition-model.html
Sample Learning Goals
(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of each
Version:
 |
| http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/20-vector-addition-a-b-c-model |
 |
| http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/20-vector-addition-a-b-c-model |
 |
| http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/20-vector-addition-a-b-c-model |
Practice
http://goo.gl/forms/2ITP4YvbZp
wanna see what others have done? click here
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
- http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang
Other Resources
- http://ophysics.com/k11.html by This email address is being protected from spambots. You need JavaScript enabled to view it.
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Parent Category: 01 Foundations of Physics
- Category: 01 Measurements
- Hits: 16997