About
7.4.3.2 Example
An Earth satellite of mass 200 kg is in stable circular motion orbit, calculate the launch speed for a distance of 2 REarth from centre of Earth.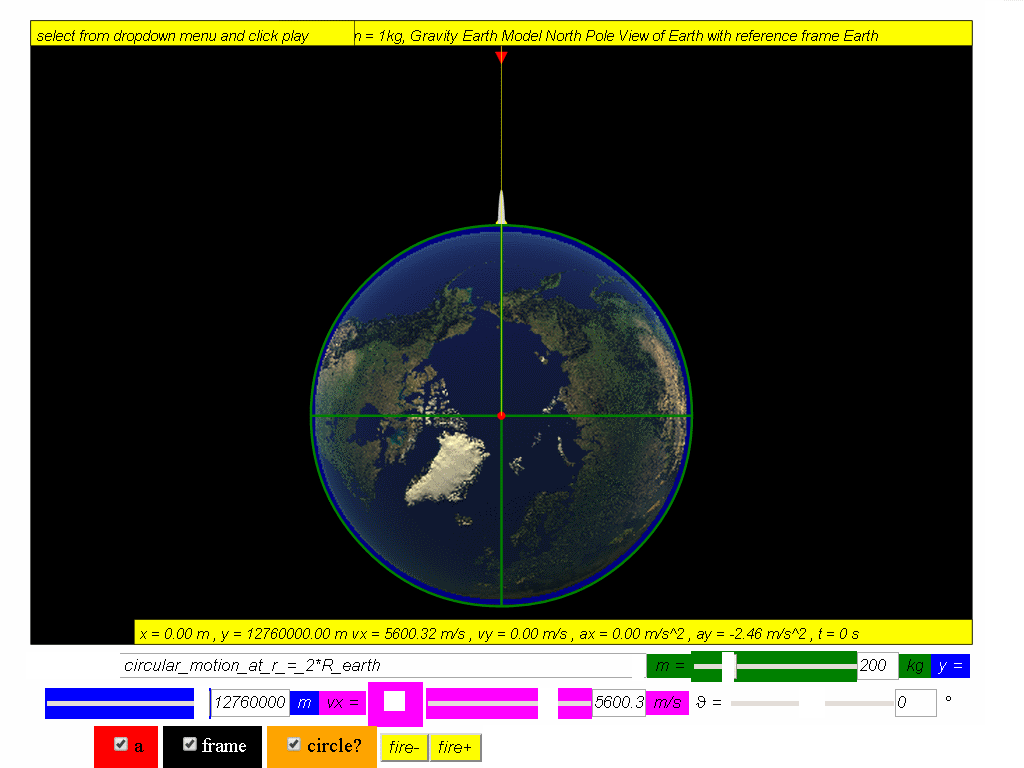
Answer: 5600 m/s
Calculate the potential energy, kinetic and total energy in this orbit.
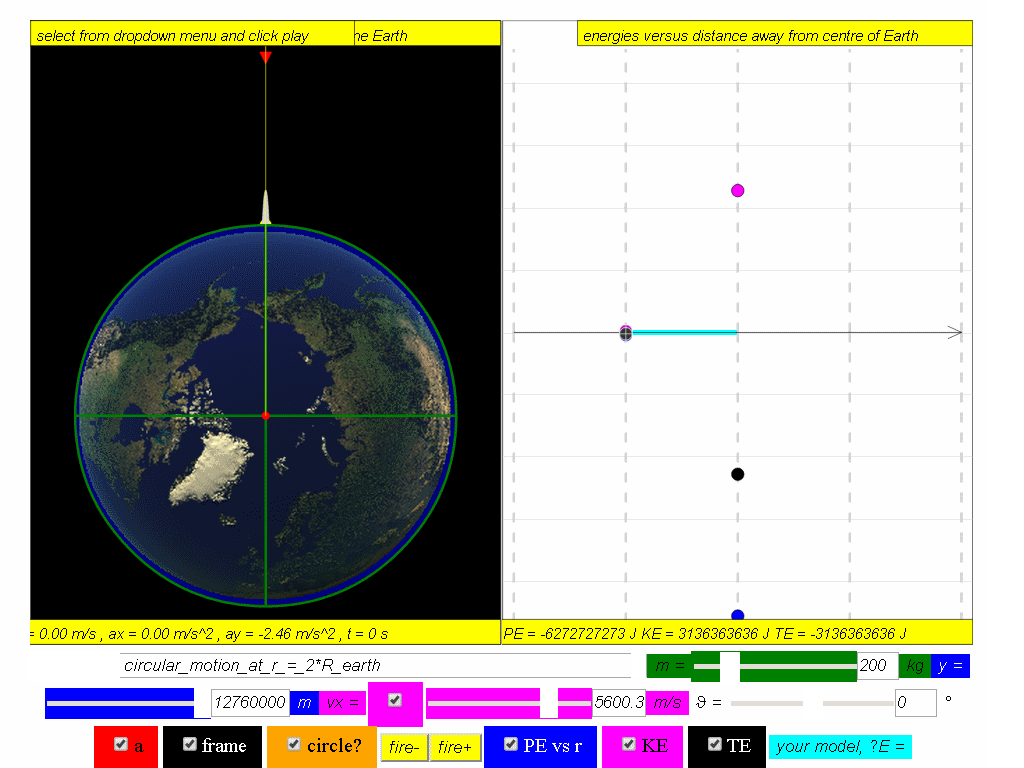
Answer: PE = -6.27x107 J, KE = 3.14x107 J, TE = -3.13x107 J.
Calculate the value of the gravitational potential at this point.
Answer: ϕ = 3.14x10 5 J/kg
Calculate the value of the gravitational acceleration at this point and state its direction.
Answer: a = 2.46 m/s2 towards centre of Earth
Calculate the value of the gravitational force on the satellite at this point and state its direction.
Answer: F = 492 N towards centre of Earth
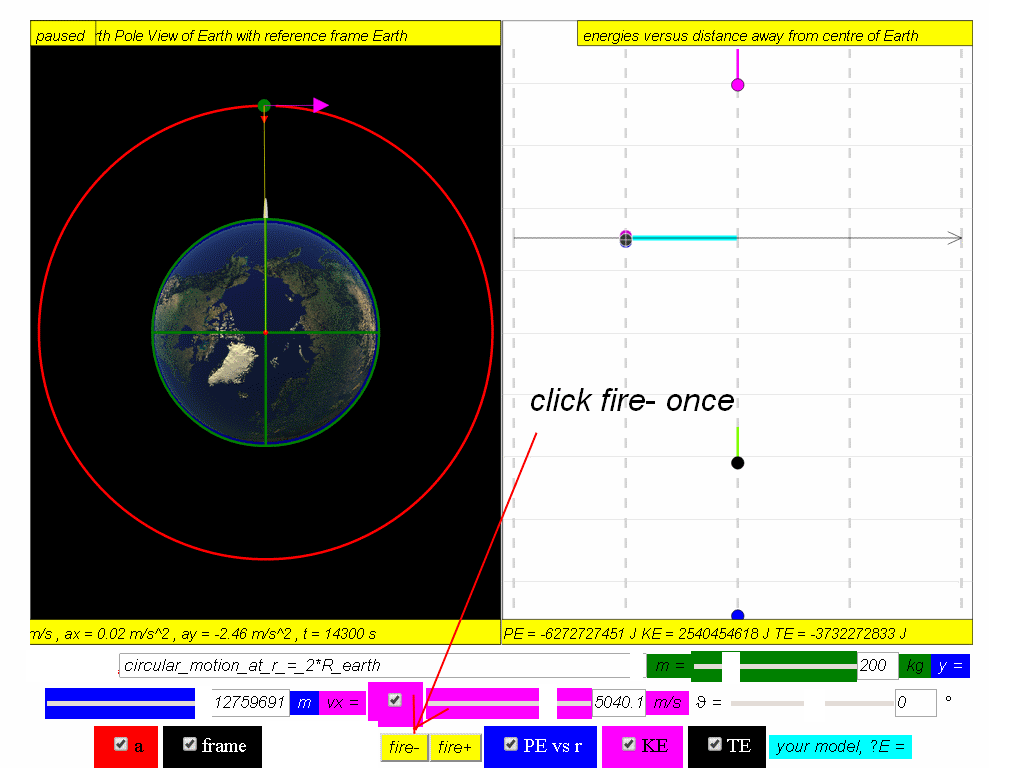
At this point of the motion, the satellite fires (click the fire- button) backward thrusters to reduce its speed.
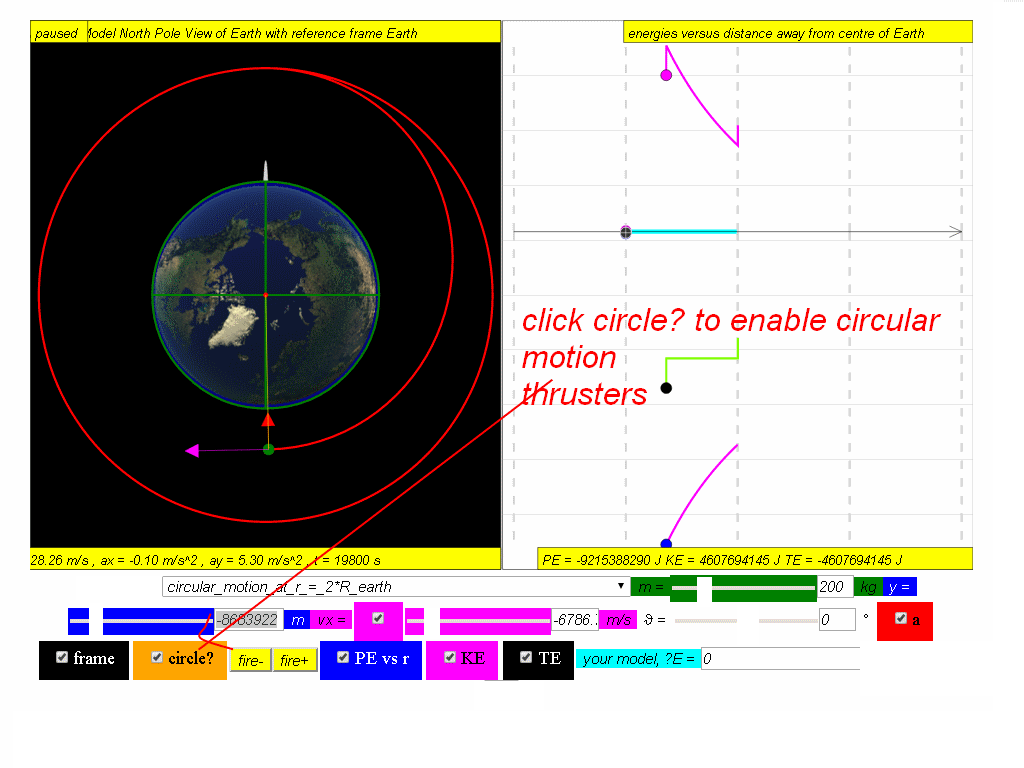
The orbits path decays to a point where it shoots some circular motion thrusters and goes on a lower circular motion.
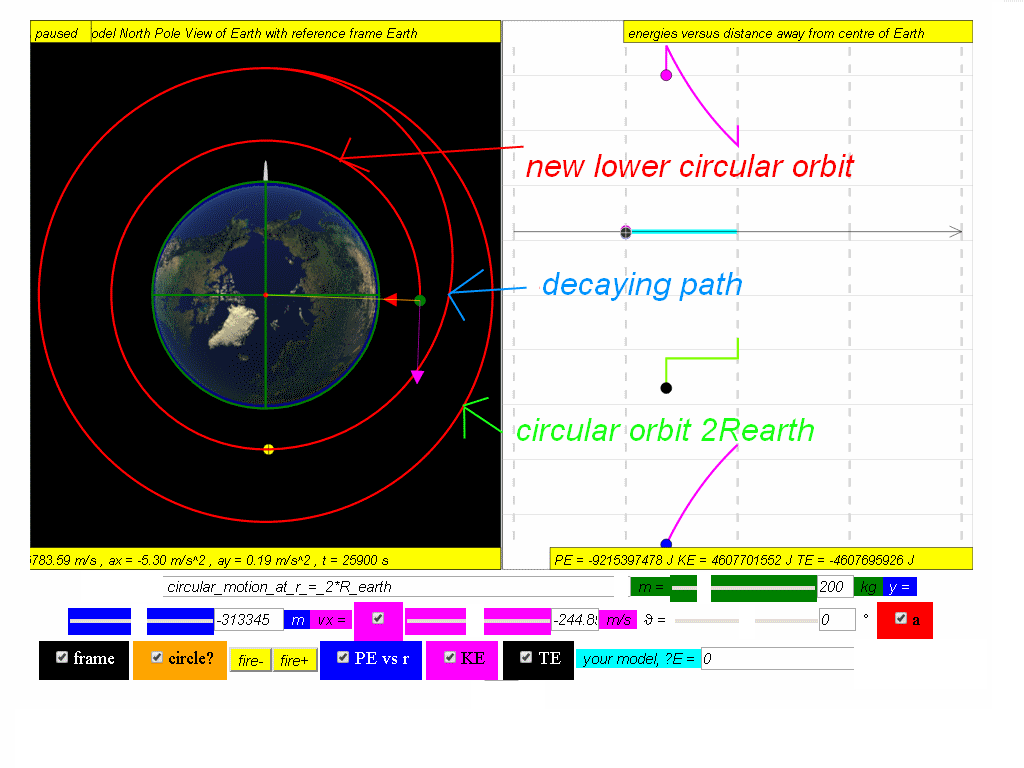
Calculate the new potential energy, kinetic and total energy in this lowered orbit, given the new radius of orbit is approximately 8.68x106 m
Answer: PE = -9.22x107 J, KE = 4.61x107 J, TE = -4.61x107 J.
Hence or otherwise, calculate the changes in the potential, kinetic and total energies of the satellite as a result of this transition. (Mass of Earth = 6.0 x 1024 kg)
Answer: ΔPE = -2.95x107 J, ΔKE = 1.47x107 J, ΔTE = -1.48x107 J.
With the diagrams below or otherwise, describe
(a) the significance of the different parts of (1,2 & 3) the graph of KE for the complete motion above.
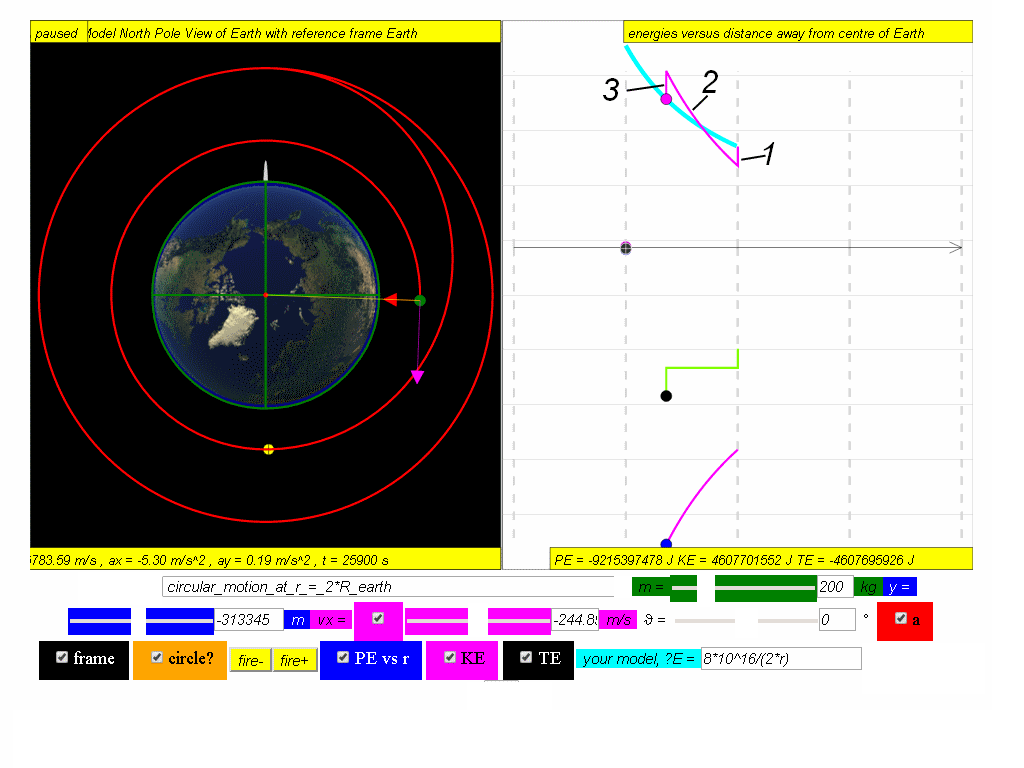
Suggested answers
1. fire reverse thrusters to begin decay path that results in decrease of KE
2. increase in speed as PE decrease and KE increase
3. fire circular motion thrusters to begin lower circular motion orbit to meet the model
(b) the significance of the different parts of the graph of PE for the complete motion above.
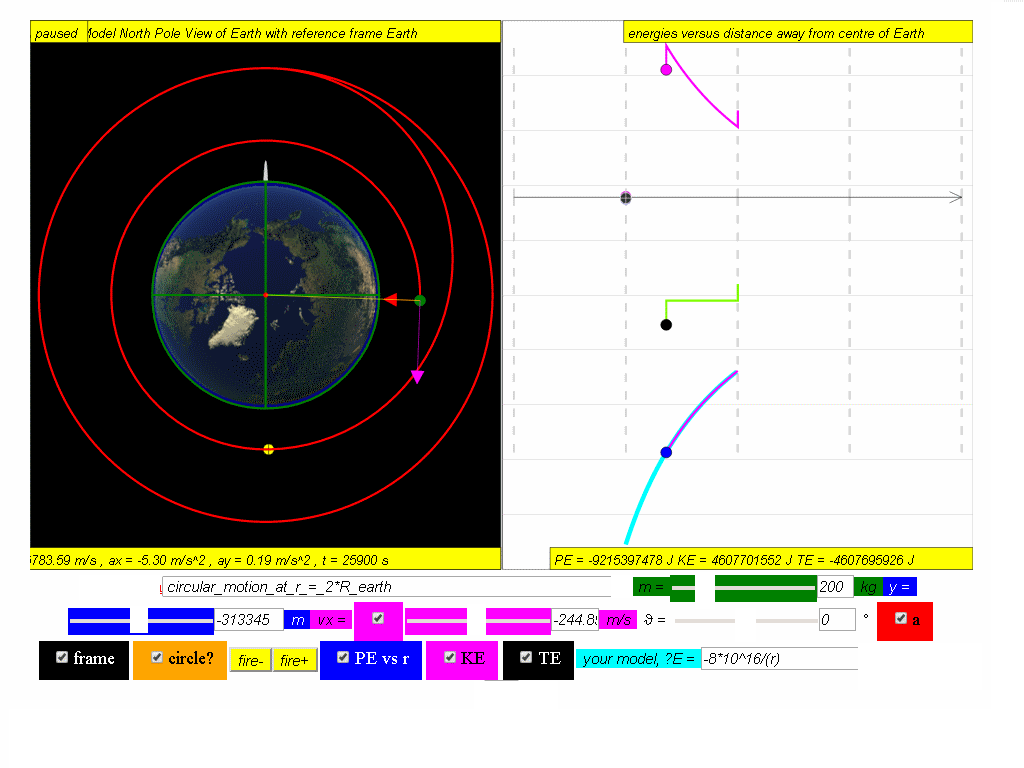
Suggested answers
the PE graph move according to the equation = mϕ from r = 2Rearth to the lower orbit from right to left
(c) the significance of the different parts of the graph of TE for the complete motion above.
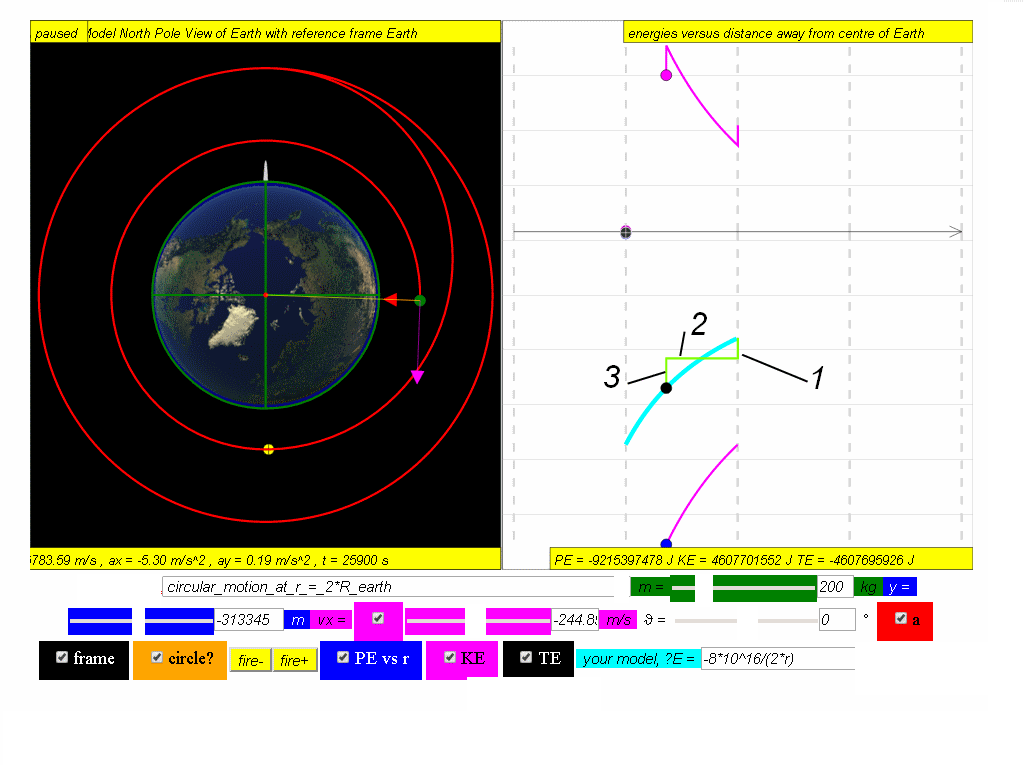
Suggested answers
1. fire reverse thrusters to begin decay path result in decrease of KE thus a corresponding decrease in TE
2. TE is constant
3. fire circular motion thrusters to begin lower circular motion orbit, results in decrease of KE and a corresponding decrease in TE to meet the model
7.4.3.2.1 Model
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
![]()

 Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang
Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang
end faq
Versions:
- http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_NewtonsMountainwee06.jar
Other resources
- http://physics.weber.edu/schroeder/software/NewtonsCannon.html
- https://scratch.mit.edu/projects/898903/ Launch Simulator by Sushiboy6
- https://www.geogebra.org/m/va3dbqyd by Tan Seng Kwang







