About
7.5 Kepler’s Third Law
7.5.1 Newton's Second Law in Circular Motion to derive Kepler’s Third Law T2 α r3

By analysing the free body diagram of a satellite in circular orbit, the
equation for Newton's Second Law is,
i.e. ΣF = mrω2
Recalling in circular motion angular velocity and its period are related
as follow,
Hence,
Which can be simplified to an equation involving T and r
This is the Kepler’s Third Law, which states that the square
of the period of an object in circular orbit is directly
proportional to the cube of the radius of its orbit. T2
α r3
7.5.1.1 Note:
The Kepler’s Third Law T2 α r3 is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it and thus it acts as the centripetal force.
7.5.1.2 Activity
Complete ICT inquiry worksheet 2 to build your conceptual understanding on Kepler’s Third Law.
7.5.1.3 Steps to support your inquiry
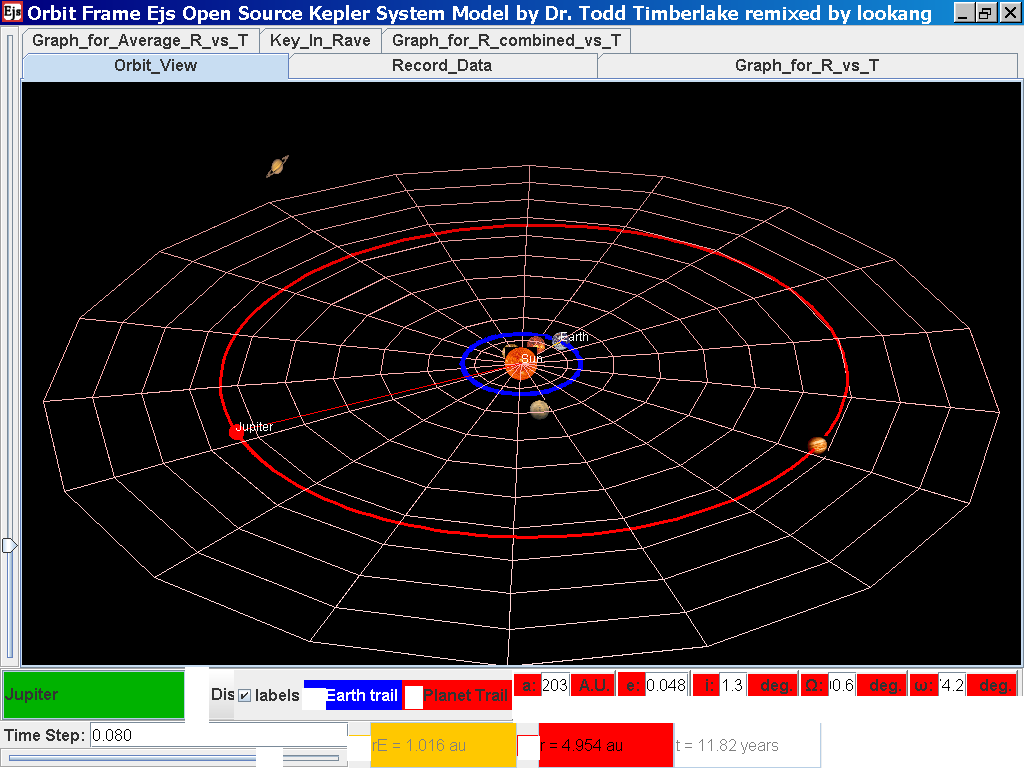
Select from the drop-down menu the planet, say Mercury to show the orbital radius and click play.
Click Pause to stop the simulation when the planet Mercury is almost at the time of 1 complete cycle or period T.
Click Step to fine tune your determination of period T, say t =0.24 years

Click on the adjacent tab Record_Data and select Record Data button to store this data on the mean radius Rm and period (time for one complete cycle) T of motion.
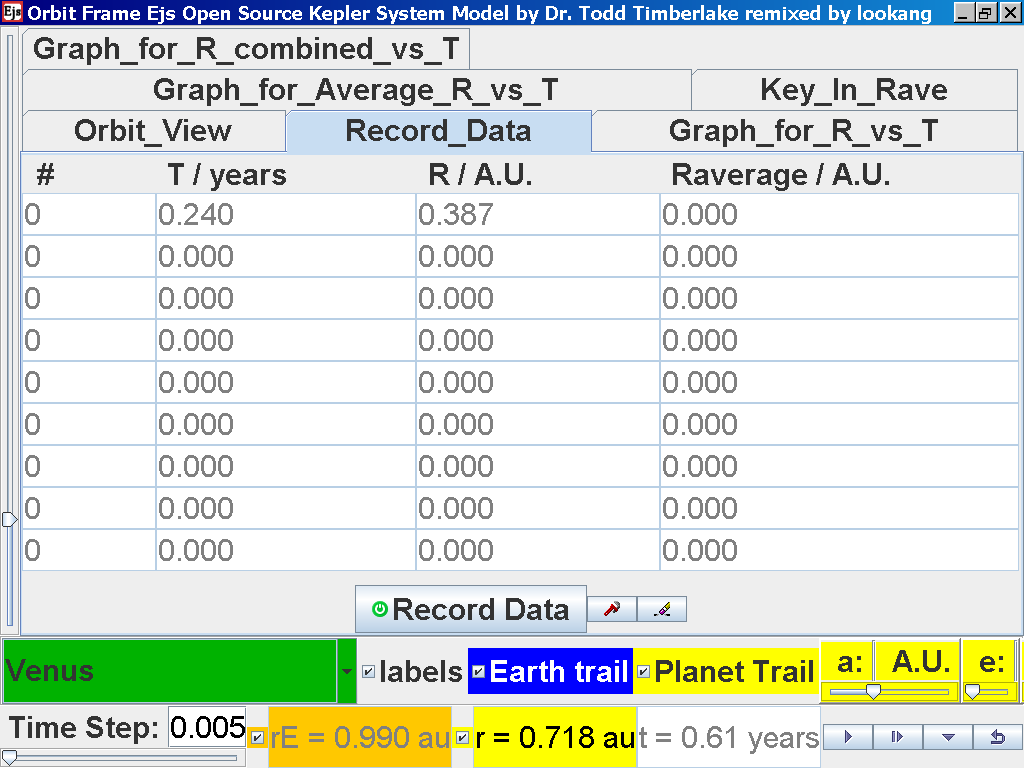
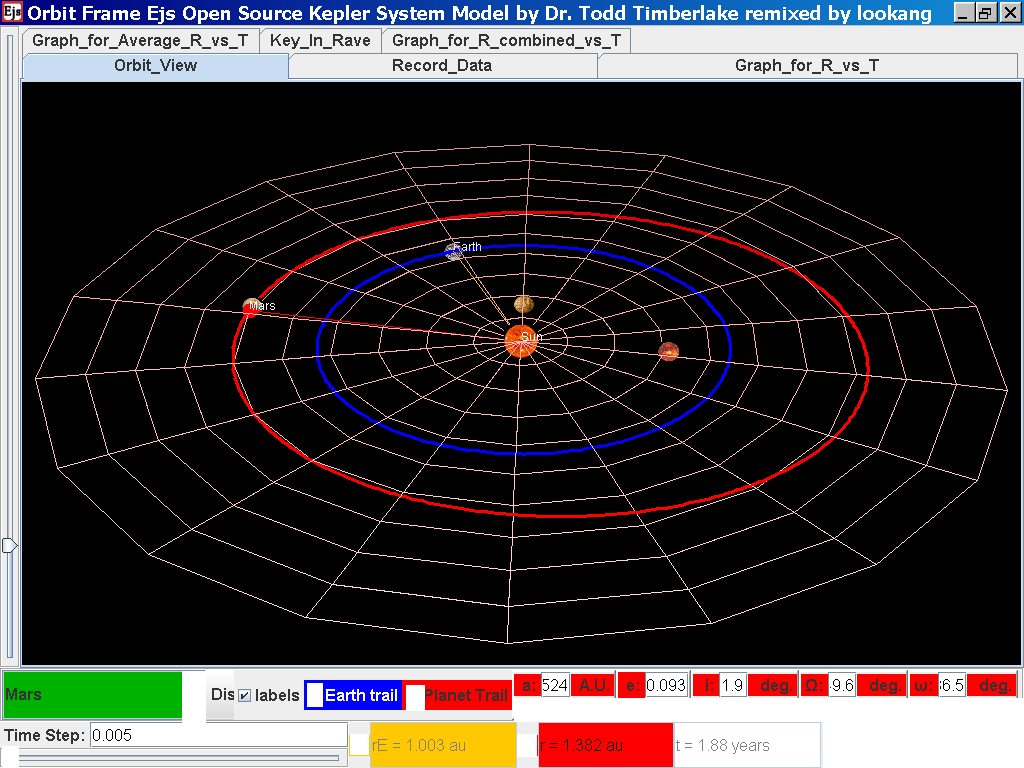
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Venus. Play the simulation for one complete cycle.
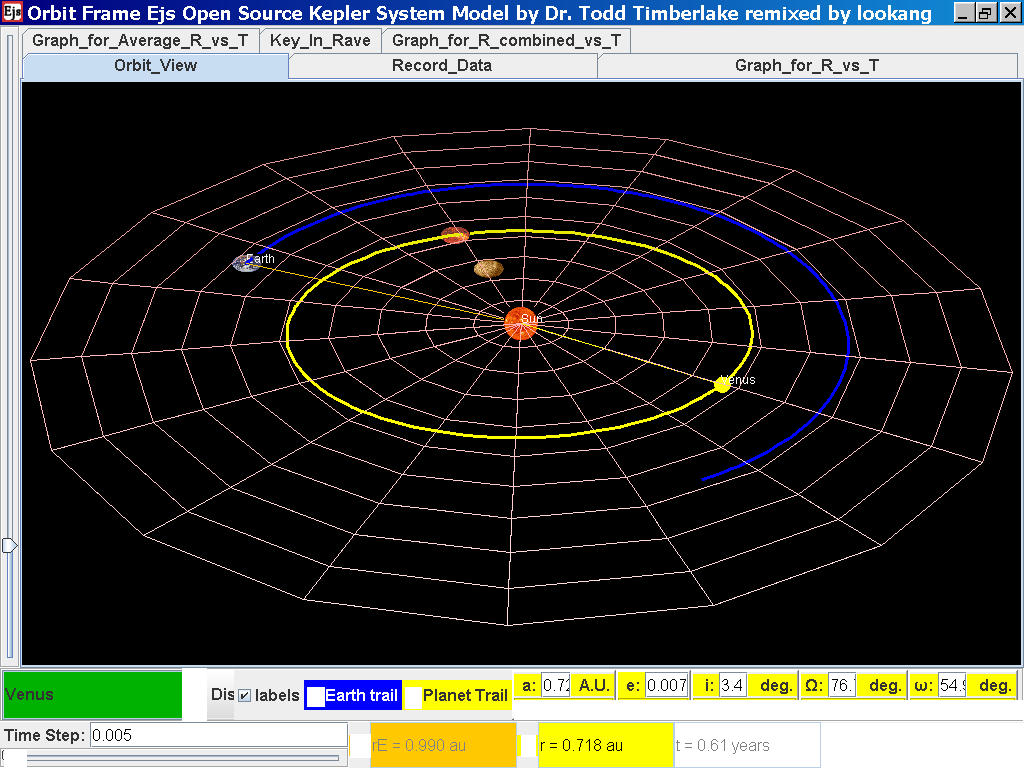
Click again on the next tab Record_Data and select Record_Data.
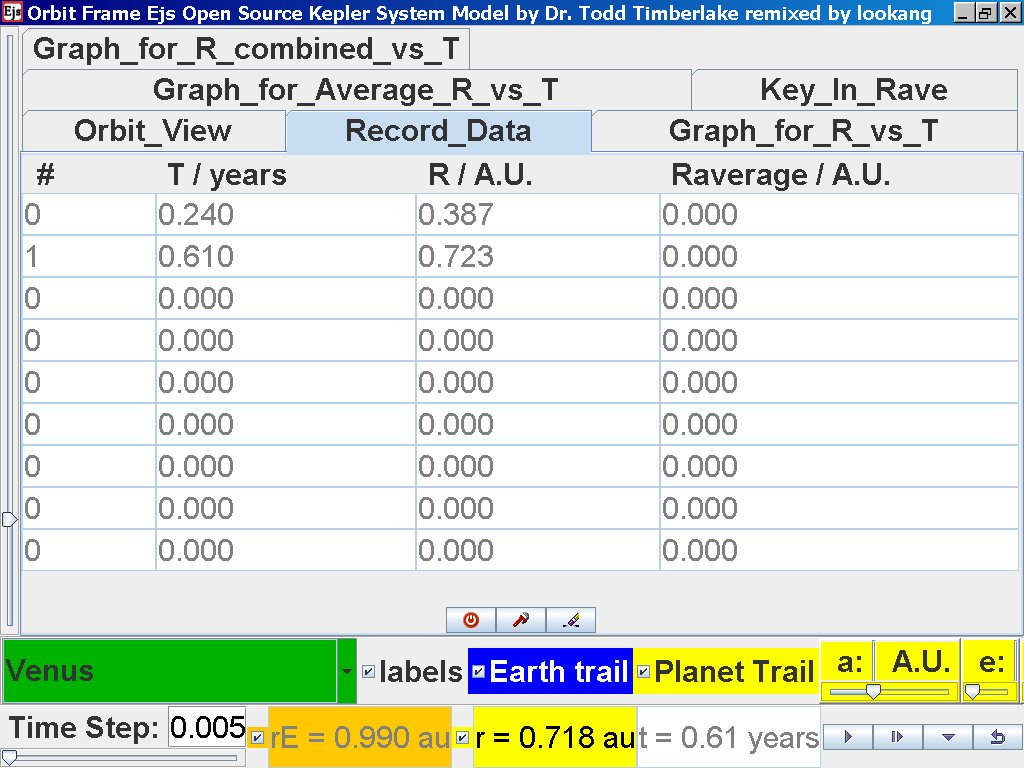
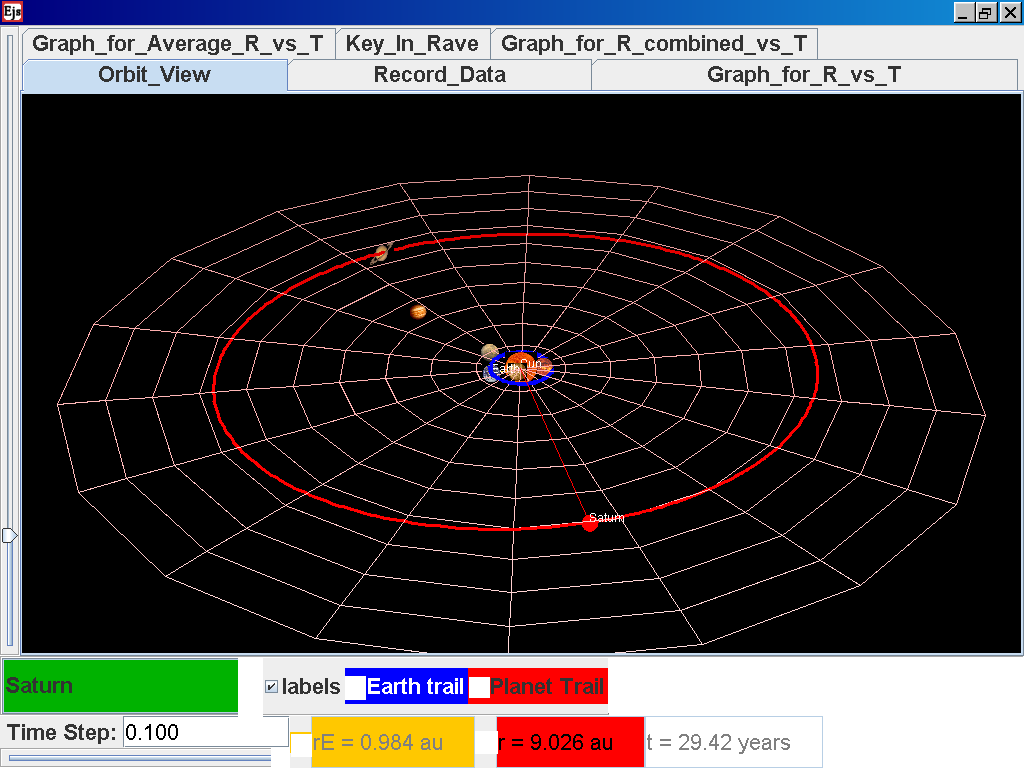
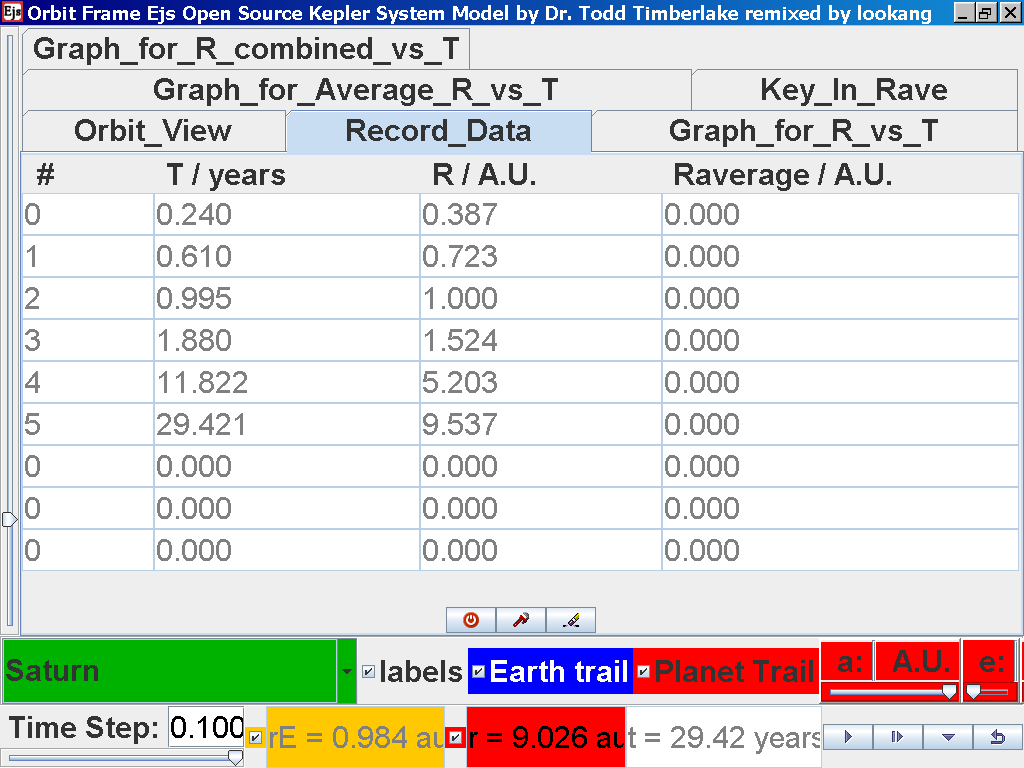
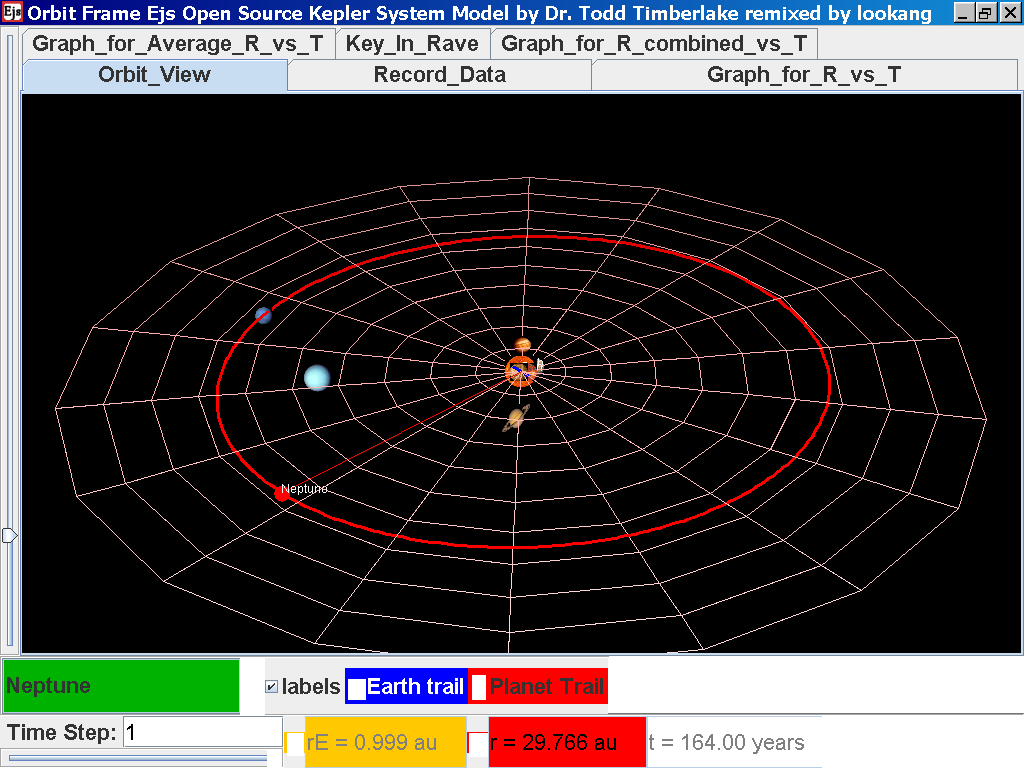
Repeat the above steps for the rest of the planets i.e. Earth, Mars, Jupiter, Saturn, Uranus, Neptune and Pluto. (Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Earth. Play the simulation for one complete cycle. )
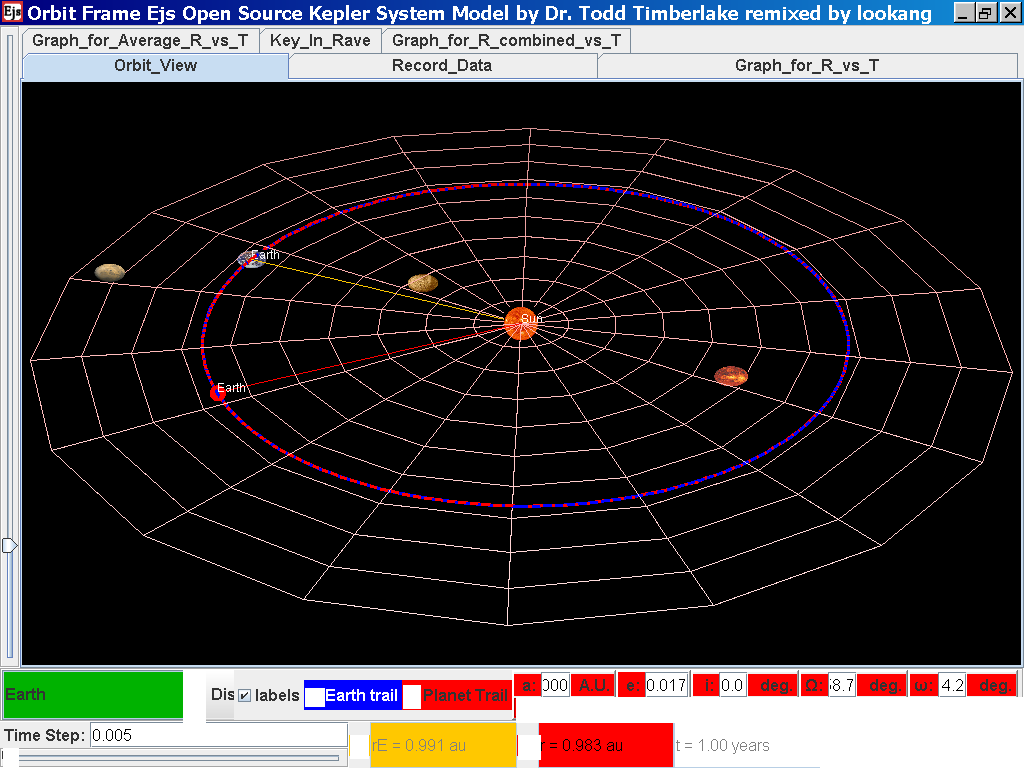
Click again on the next tab Record_Data and select Record_Data.
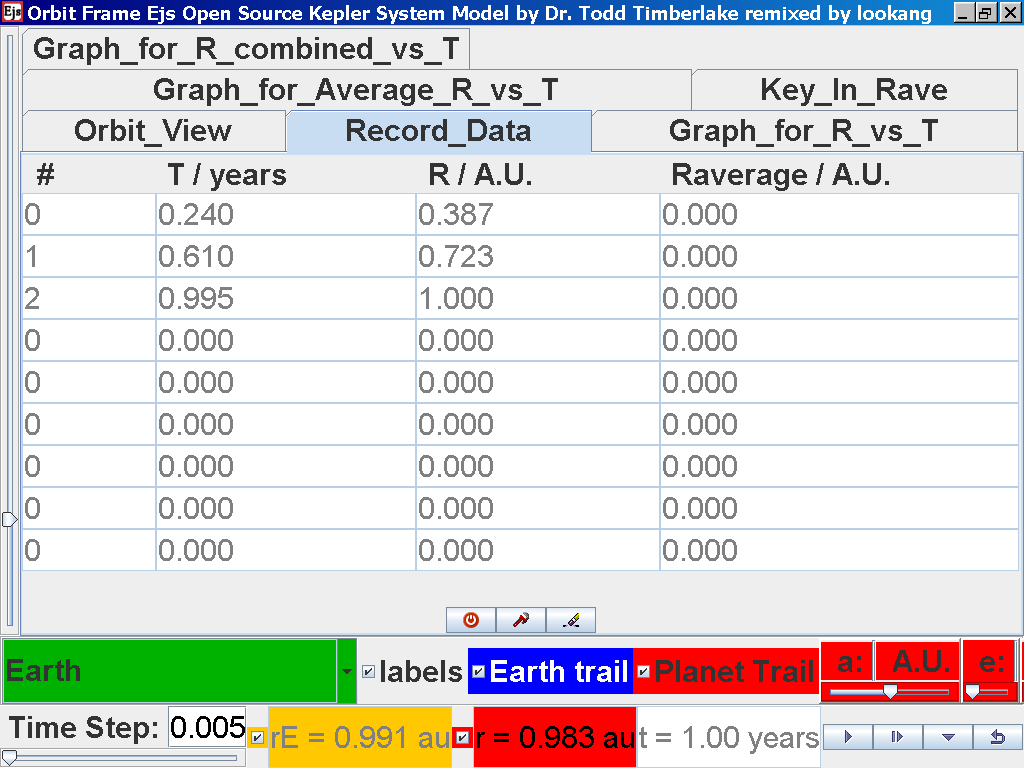
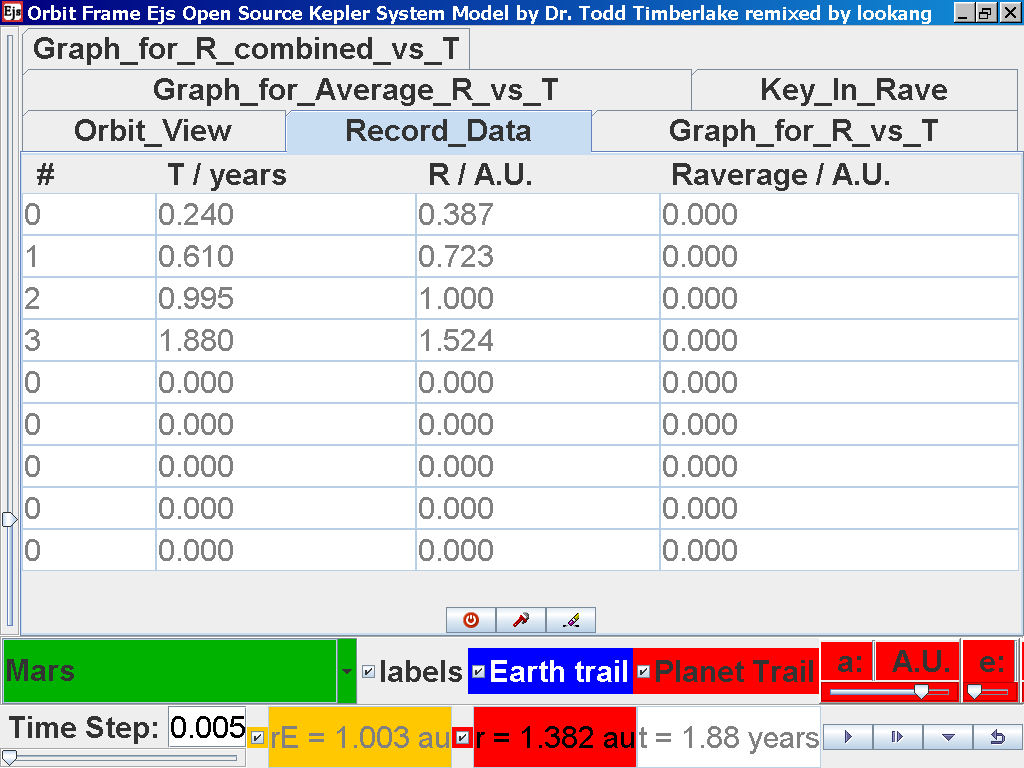
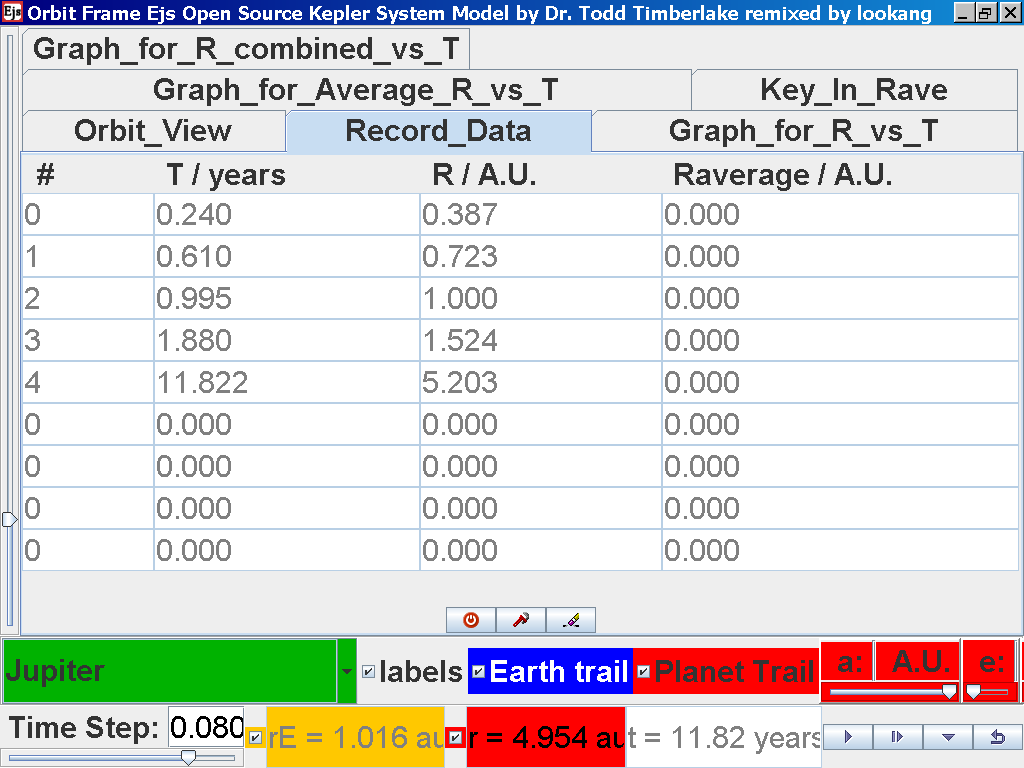
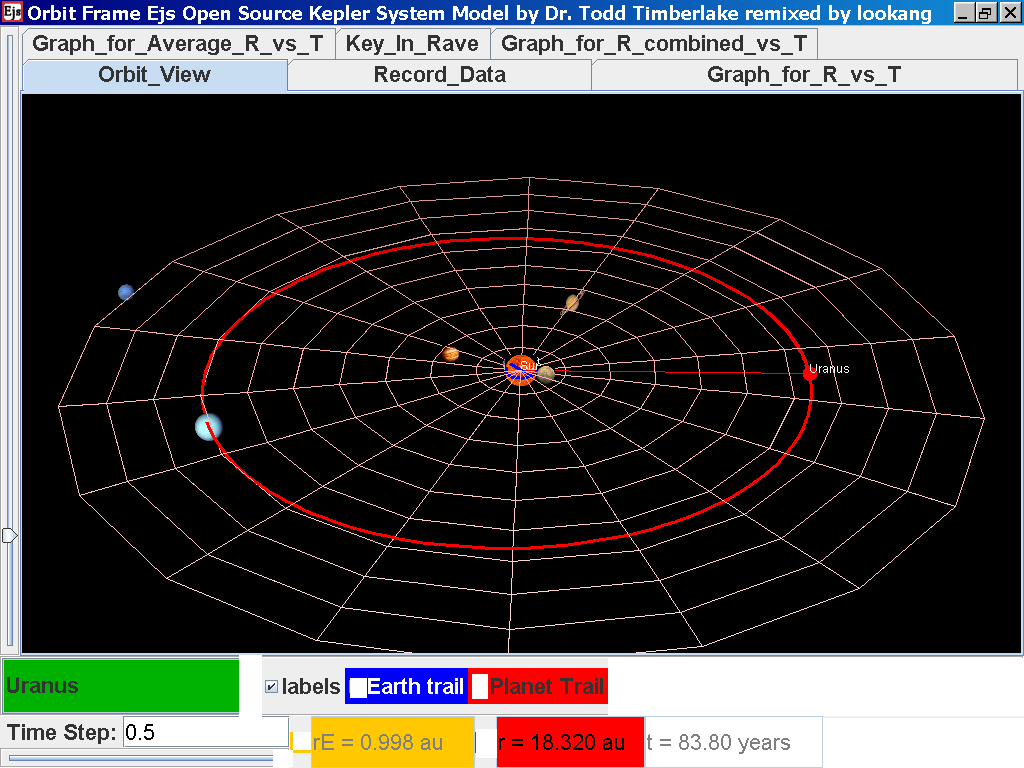
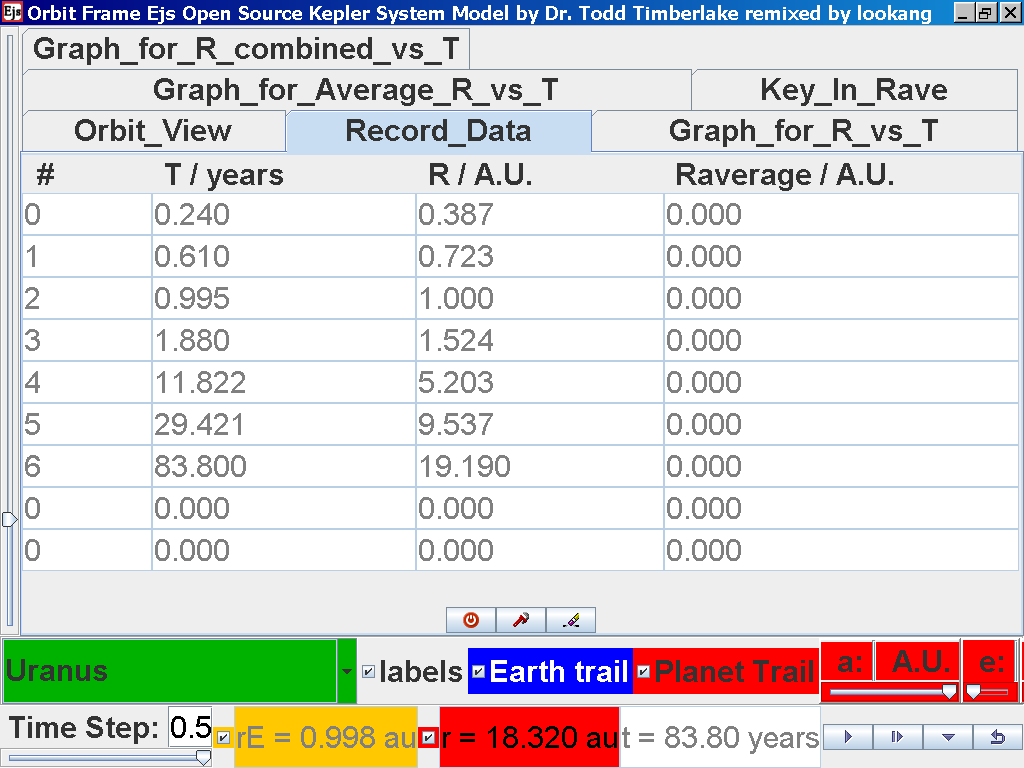
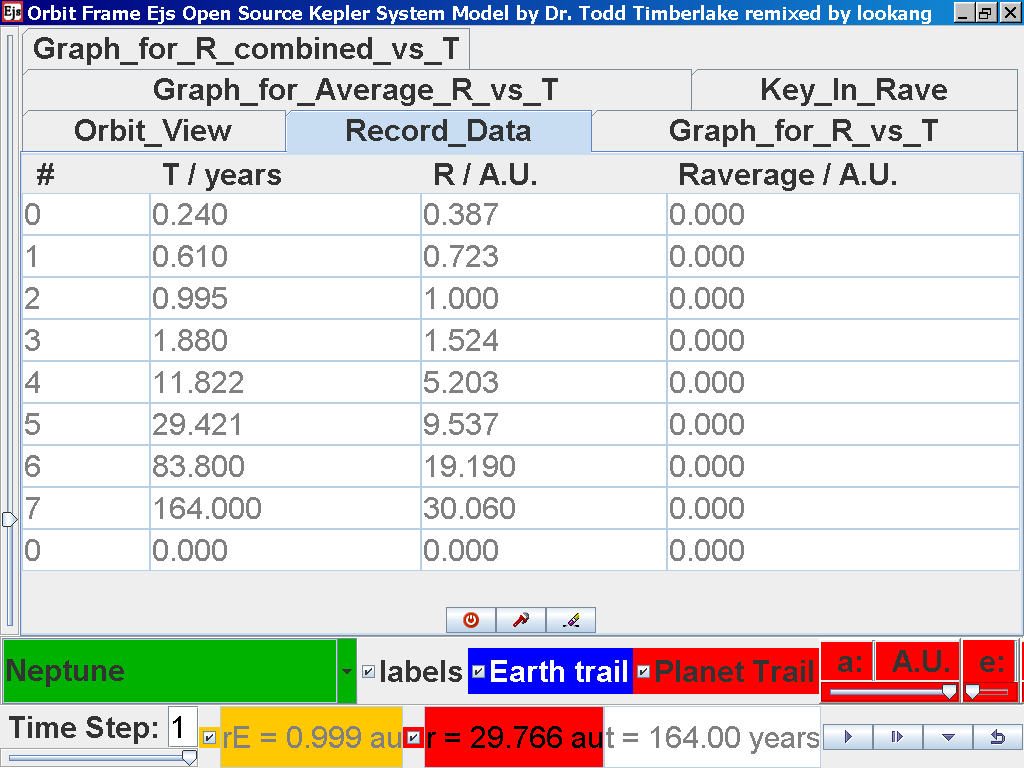
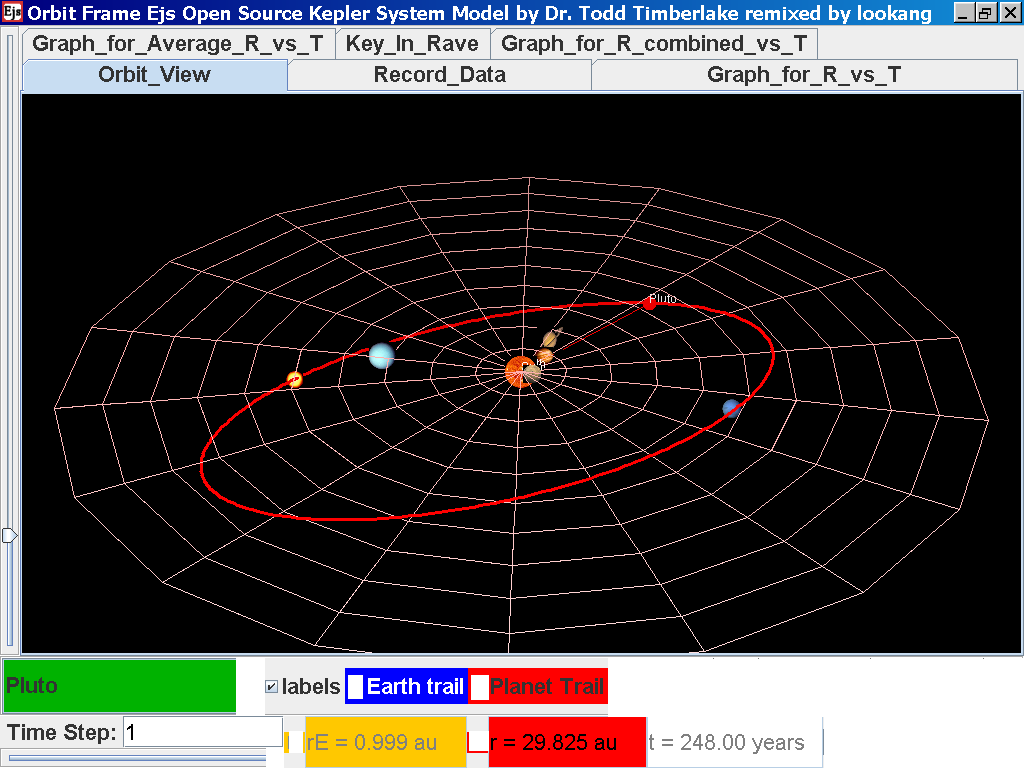
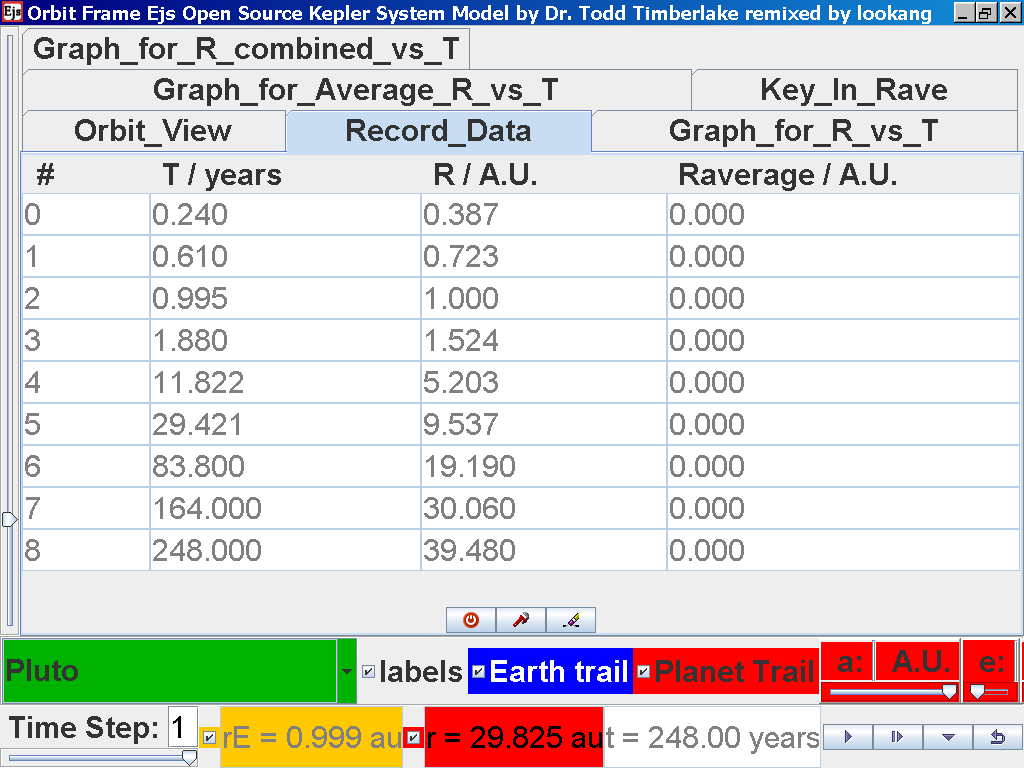
Notice all the data on the actual T /years recorded by you are slightly different compared to the mean radius of orbits R has units of A.U. (astronomical units) where by 1 A.U. = mean distance of Earth to Sun.
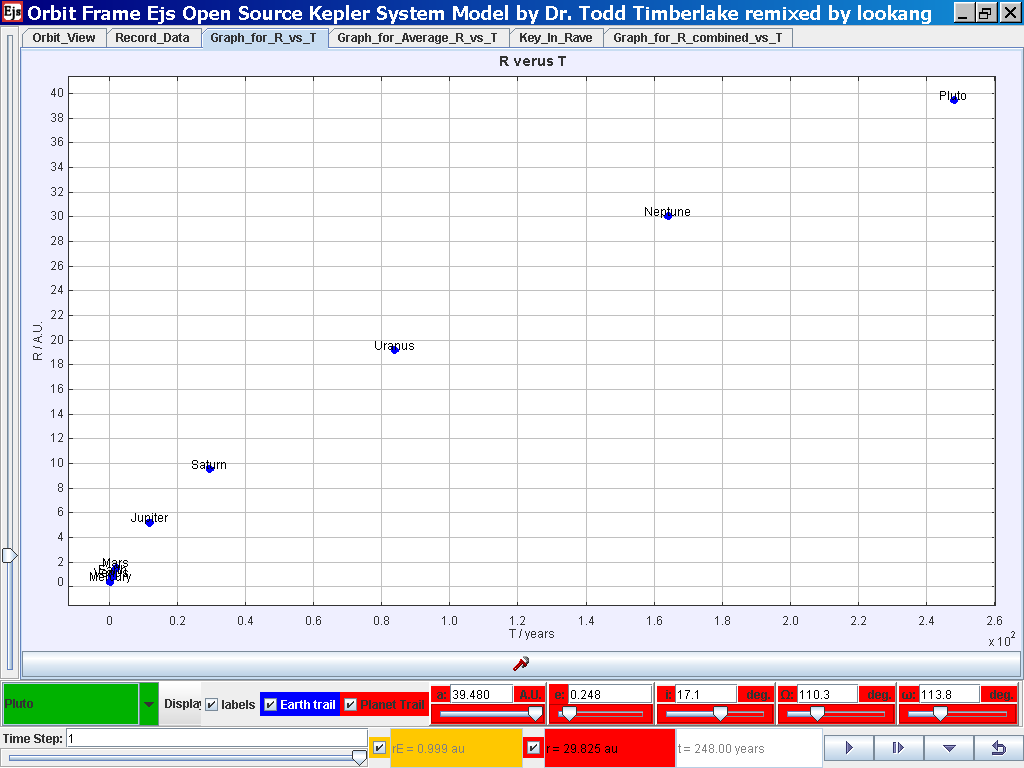
Select the tab Graph_for_R_vs_T and the simulation automatically plots the data.
Click on the Data Analysis Tool to bring up the following pop up view for further trend fitting.
Select the Data Builder Button at the top right corner
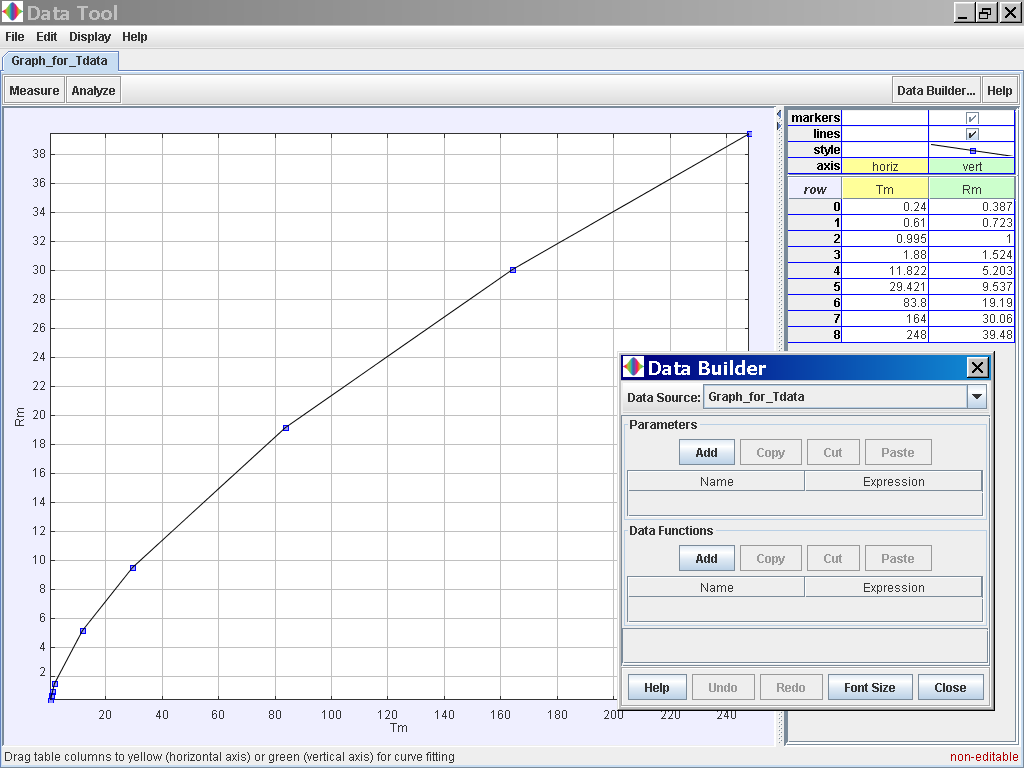
Click on the Data Function Add button to add your own functions such as T2 for Tmean2 and R3 for rmean3.
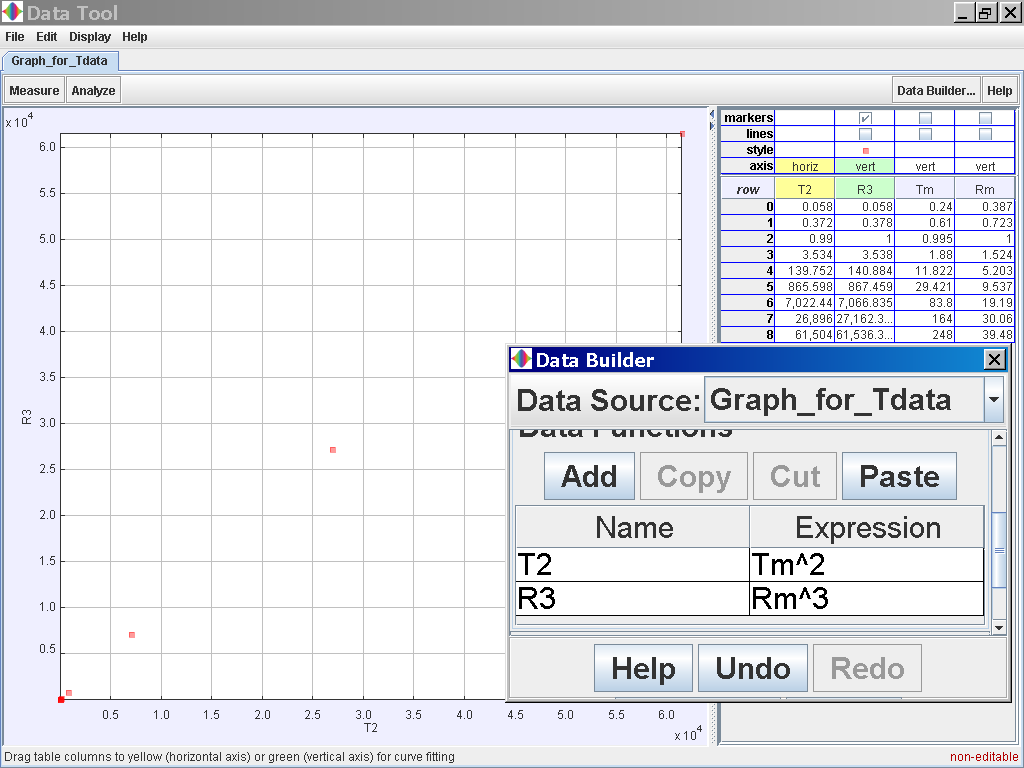 Click on the Analyse
button on the top left corner and select the Linear Fit Option of which the
data of T2 and R3 is related by the following line fit
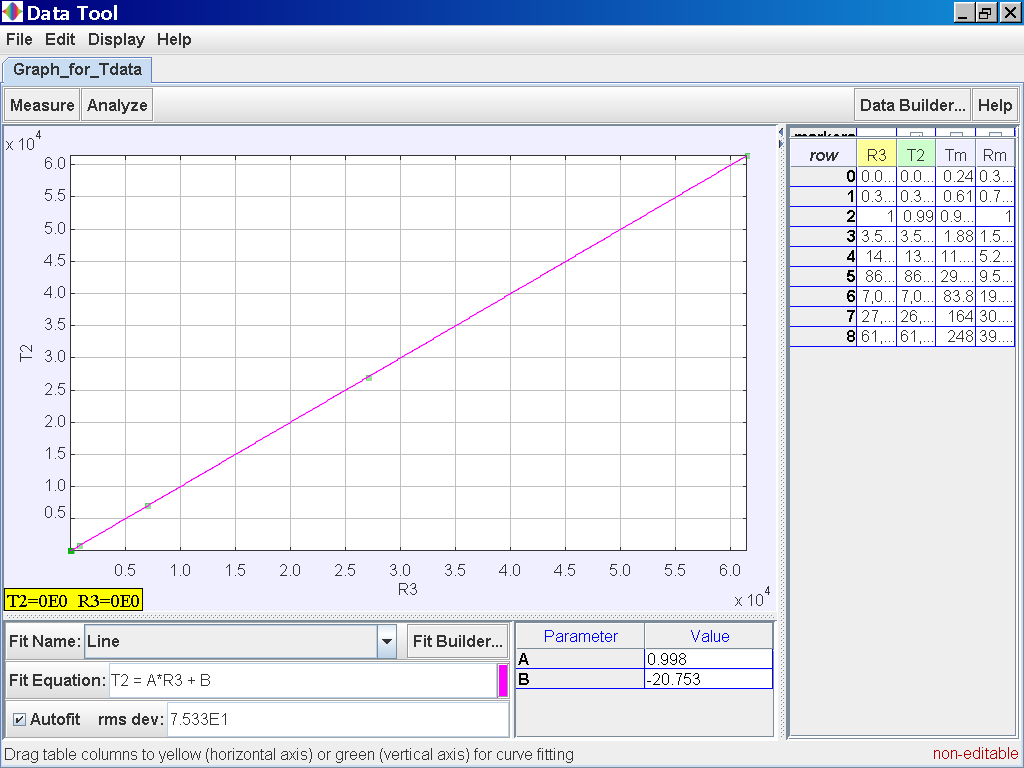
Click on the Analyse
button on the top left corner and select the Linear Fit Option of which the
data of T2 and R3 is related by the following line fitT2 = 0.998 R3 -20.753 which suggests T2 α r3
Alternatively, you can also try to plot log (T) versus log (R)
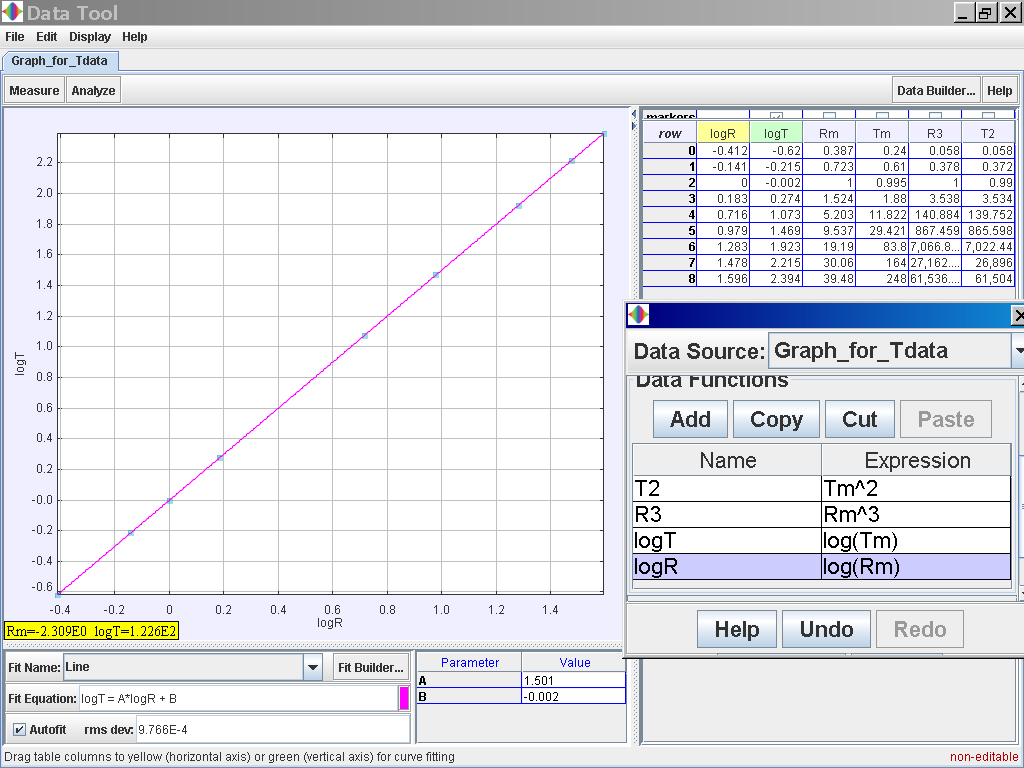
Notice that log (T) = 1.501 log (R) -0.002 which suggests the relationship of T α r1.5 or simply T2 α r3
7.5.1.4 YouTube
- https://youtu.be/jt88koyZQuw Discovering Kepler 3rd System by inquiry collect data like scientists
7.5.1.5 Java simulation for the full inquiry described above
7.5.1.6 Model, you can record down the time for each planet's one revolution to determine if T2 α r3 is valid
- https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_gravity09/gravity09_Simulation.xhtml
- http://iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/08-gravity/241-gravity09
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

![]() lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); Todd TimberLake
lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); Todd TimberLake
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.gravity091app597842
Kepler’s Third Law
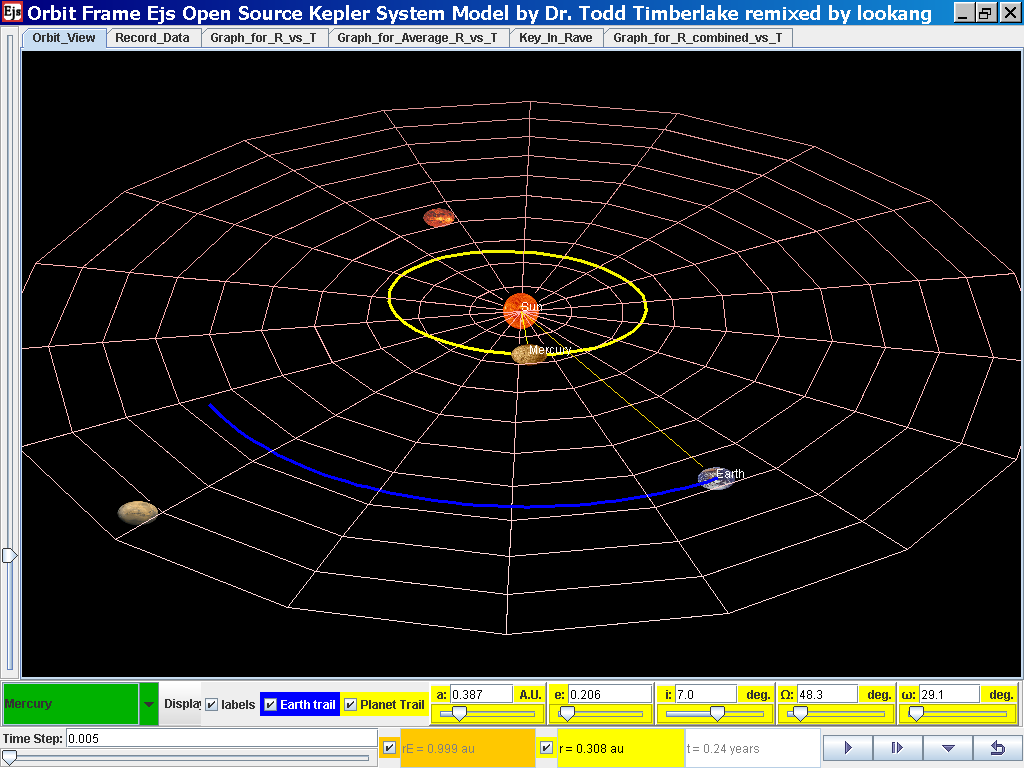
It was stated that the gravitational force acting on a satellite in orbit is the centripetal force to keep it in circular motion.
i.e. ΣF = mrω2
G m M r 2 = m r ω 2
recalling in circular motion, ω = 2 πT
Hence, G m M r 2 = m r ω 2 = m r( 2 π T ) 2
can be simplified to an equation involving T and r
T 2 = 4 π 2 G M r 3
This is the Kepler’s Third Law, which states that the square of the period of an object in circular orbit (i.e. the gravitational force acts as the centripetal force) is directly proportional to the cube of the radius of its orbit. T2 α r3
Note:
• The Kepler’s Third Law is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it to act as its centripetal force.
Complete ICT inquiry worksheet 2 to build your conceptual understanding on the Kepler’s Third Law.
This series of screenshot serves to guide your inquiry
Select from the drop-down menu the planet, say Mercury to show the orbital radius and click play.
Click Pause the simulation when the planet Mercury is almost at the time of 1 complete cycle or period T.
Click Step to fine tune your determination of period T, say t =0.24 years

Click on the adjacent tab Record_Data and select Record Data button to store this data on the mean radius Rm and period (time for one complete cycle) T of motion.
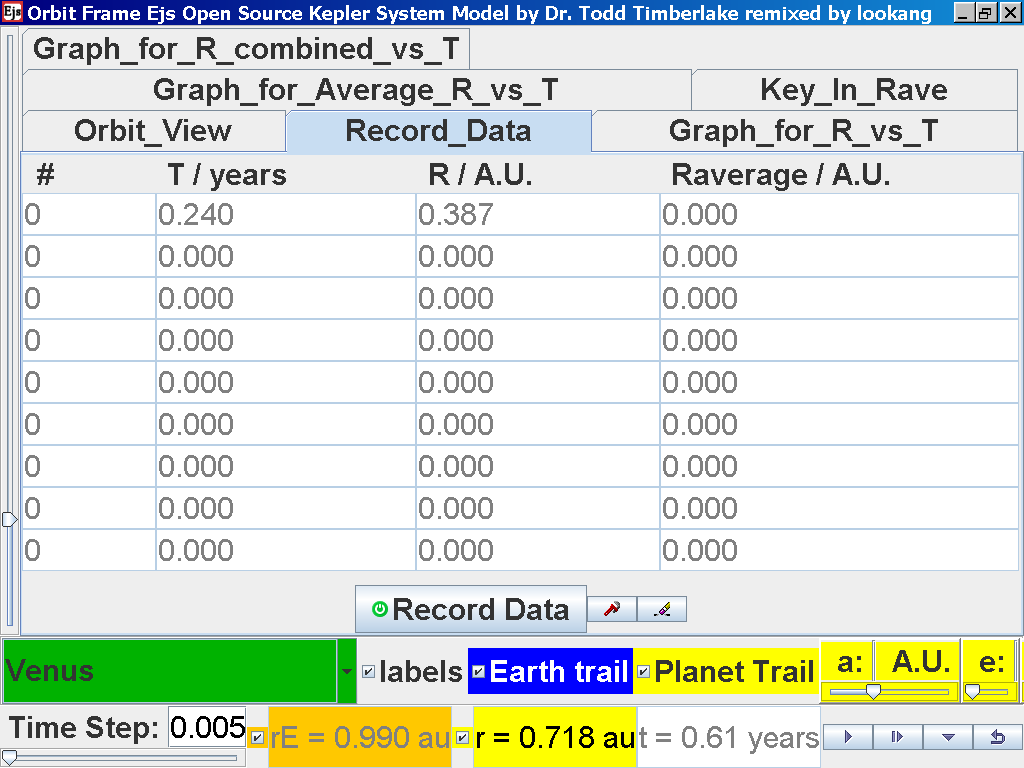
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Venus. Play the simulation for one complete cycle. 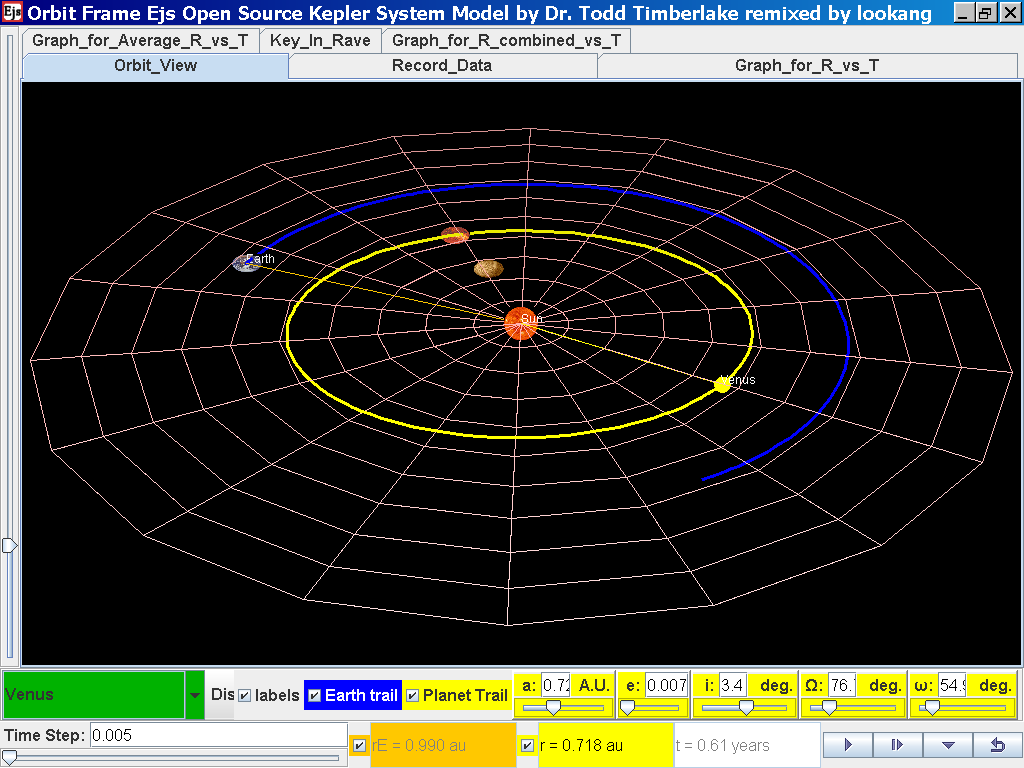
again click on the next tab Record_Data and select Record_Data. 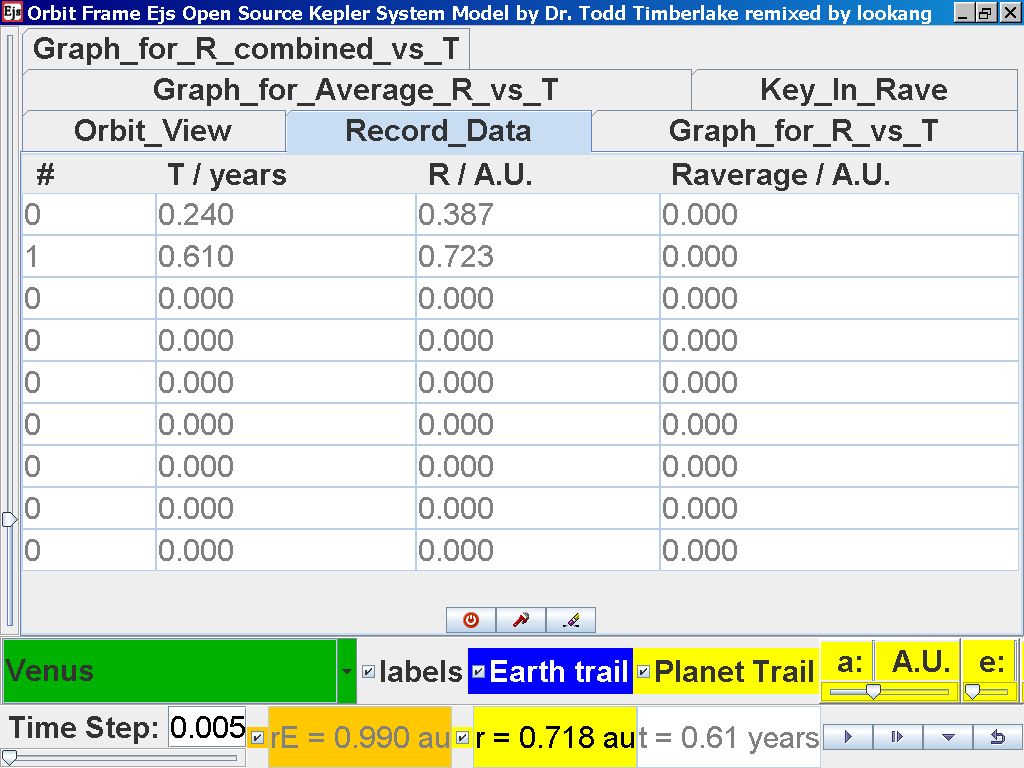
Now the steps need to be repeated for the rest of the planets. Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Earth. Play the simulation for one complete cycle. 
again click on the next tab Record_Data and select Record_Data. 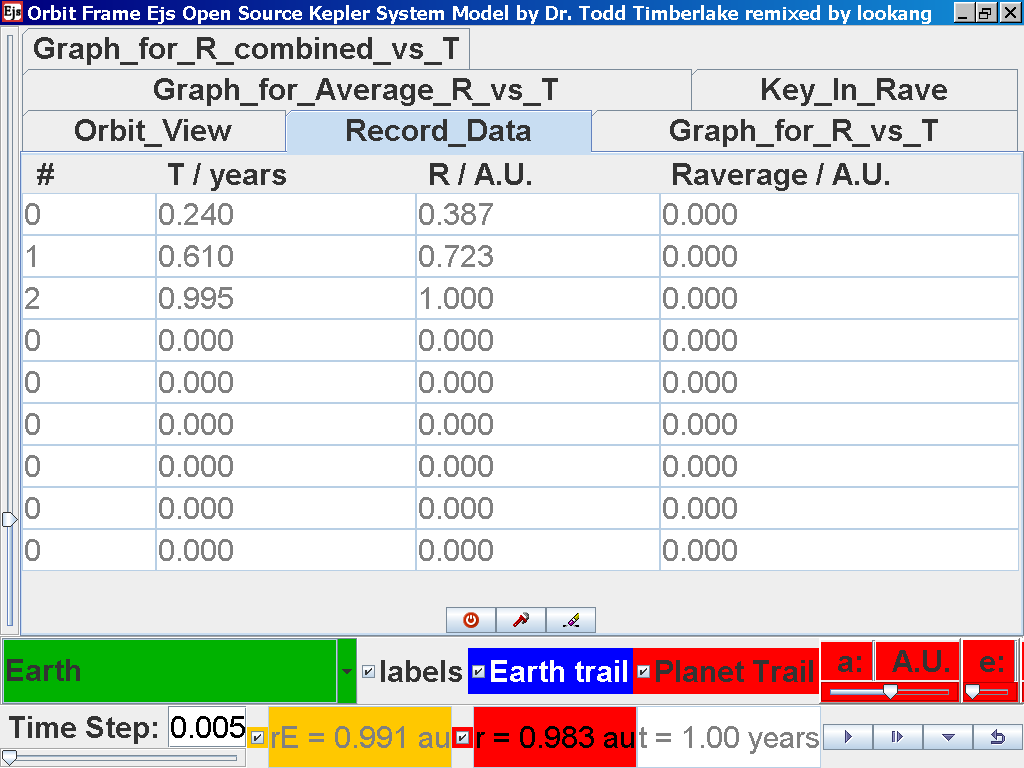
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Mars. Play the simulation for one complete cycle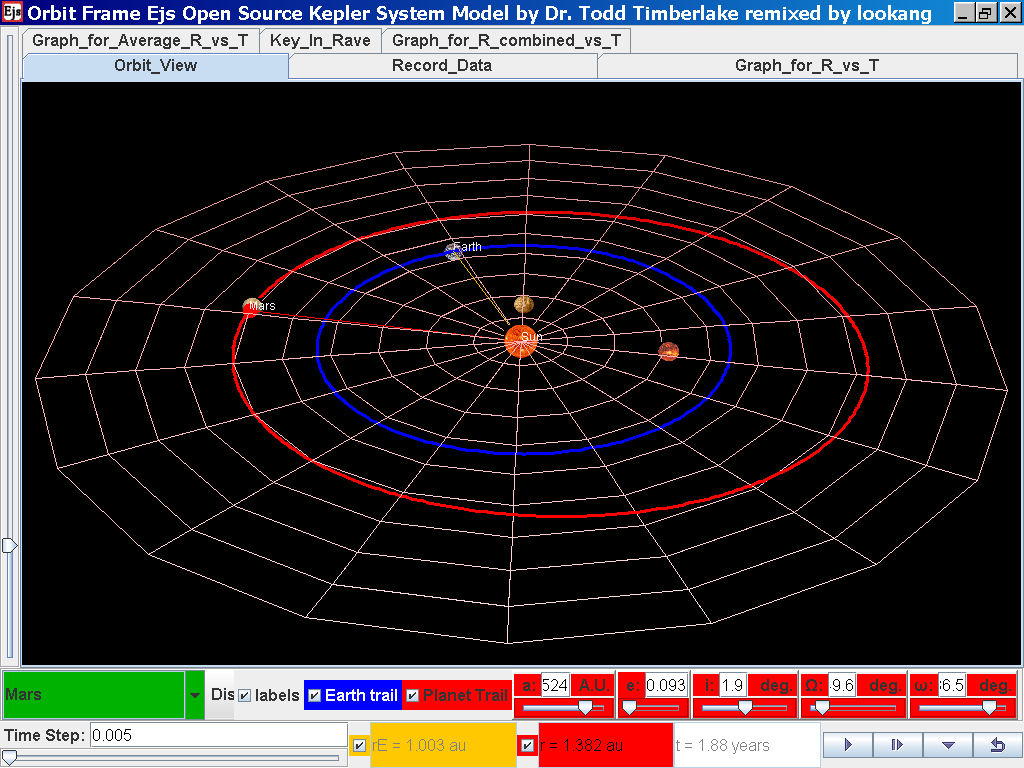
again click on the next tab Record_Data and select Record_Data. 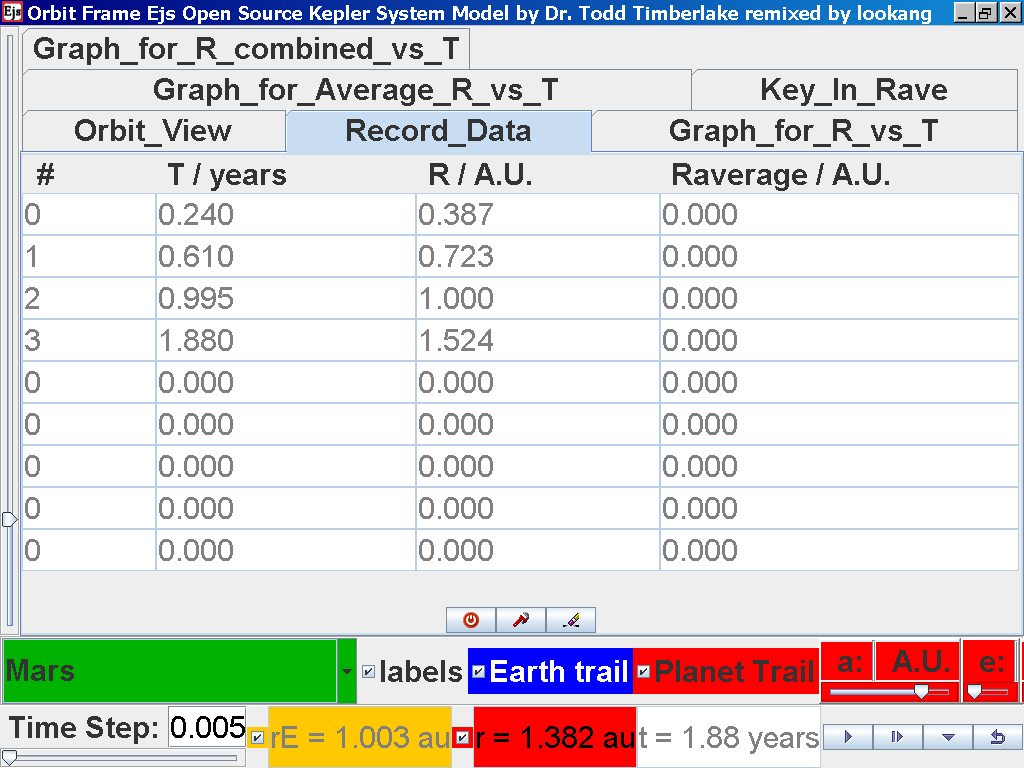
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Jupiter. Play the simulation for one complete cycle and increase the time step = 0.08 years reduces the time needed to wait for one cycle.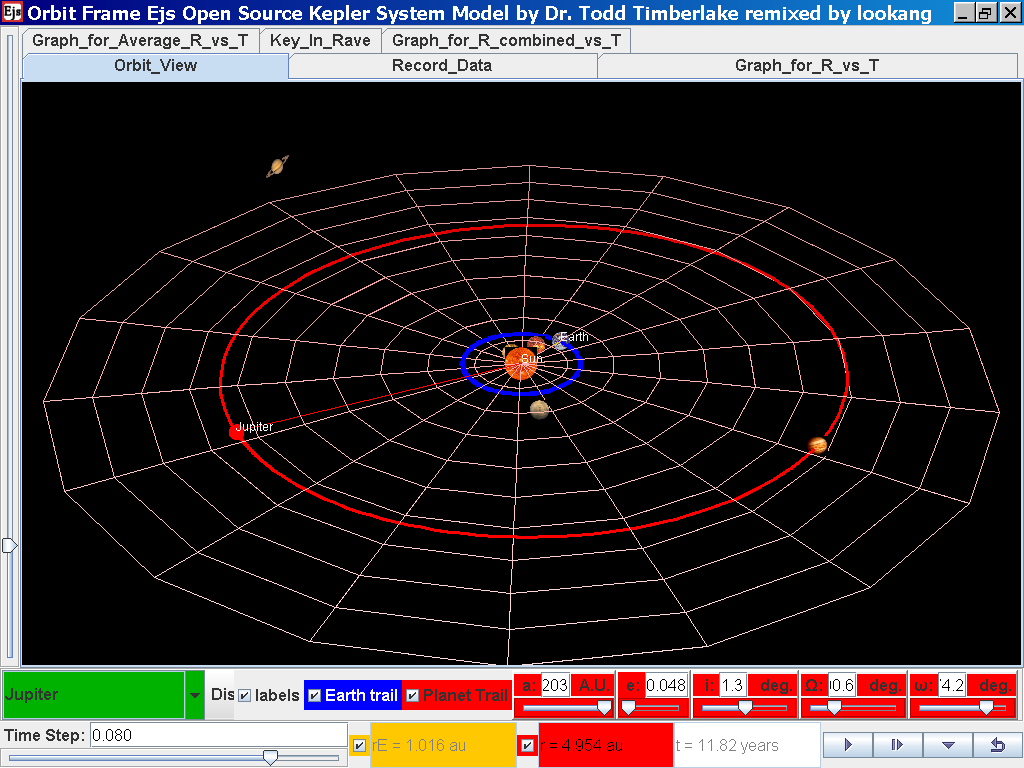
again click on the next tab Record_Data and select Record_Data. 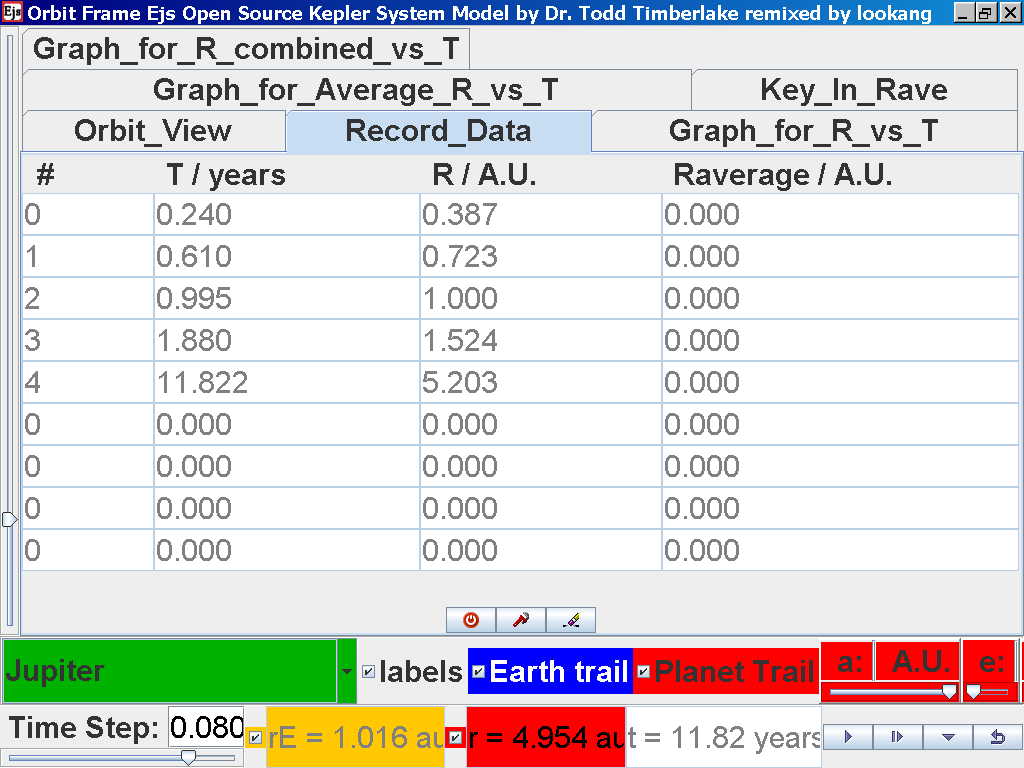
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Saturn. Play the simulation for one complete cycle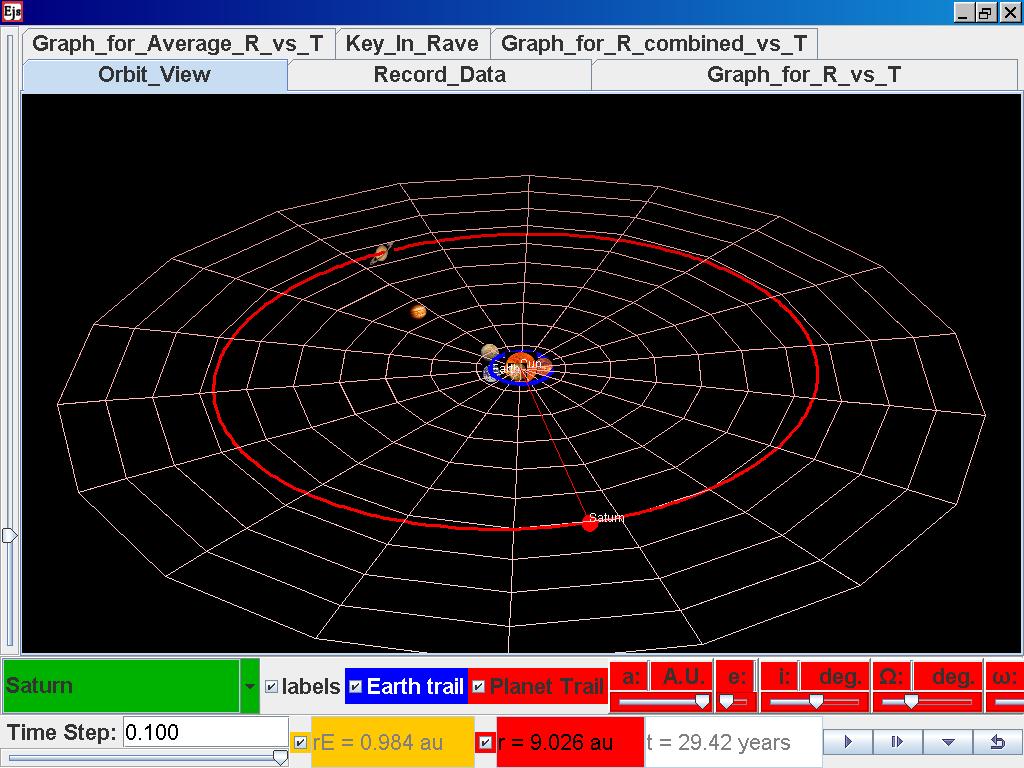
again click on the next tab Record_Data and select Record_Data. 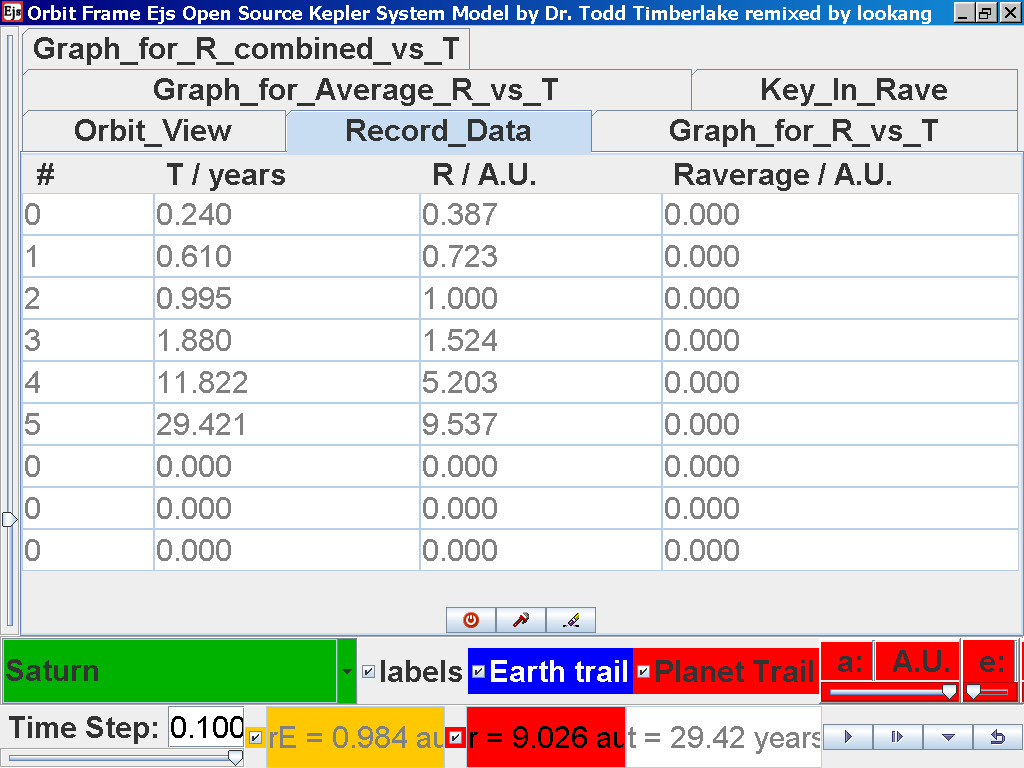
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Uranus. Play the simulation for one complete cycle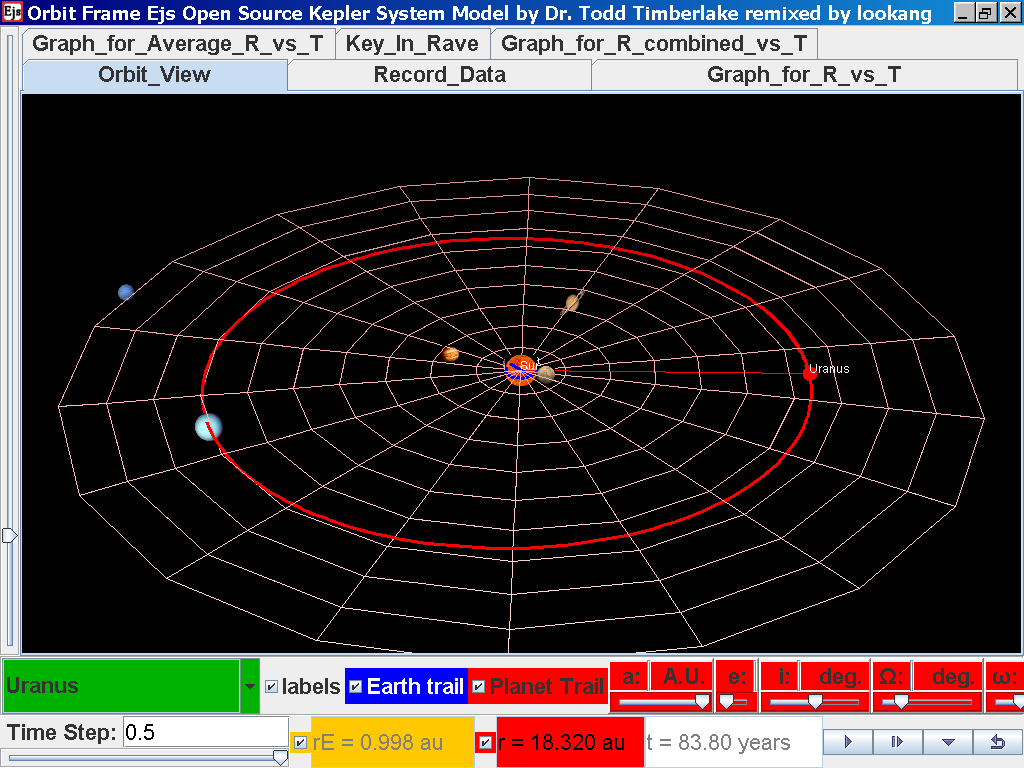
again click on the next tab Record_Data and select Record_Data. 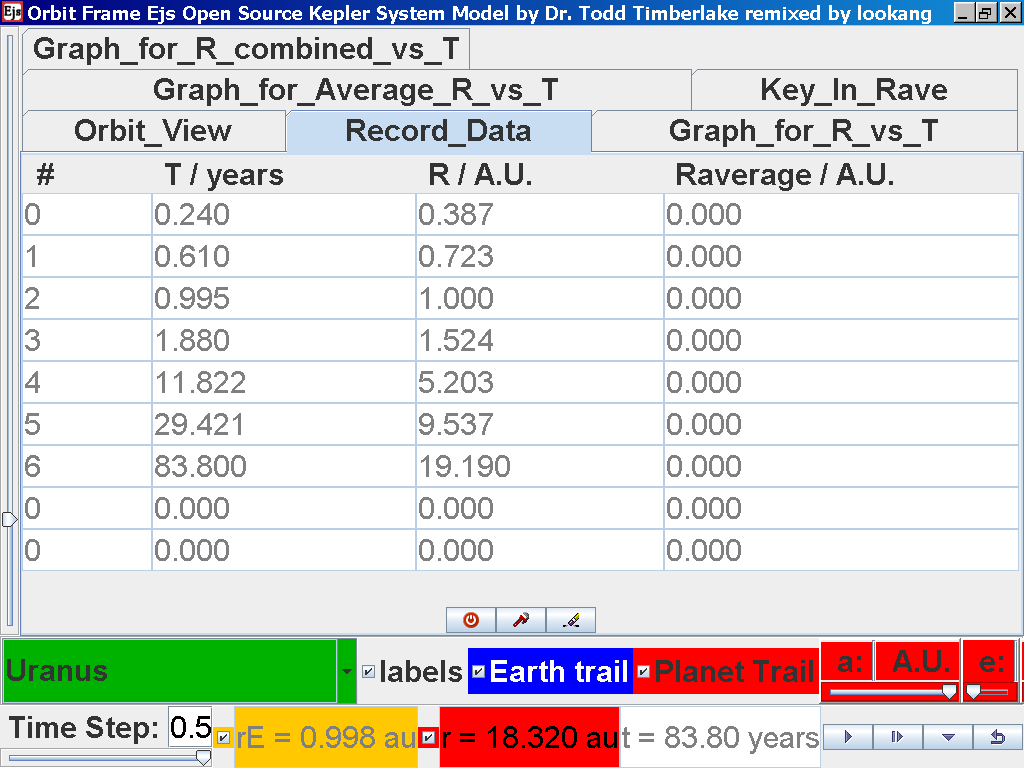
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Neptune. Play the simulation for one complete cycle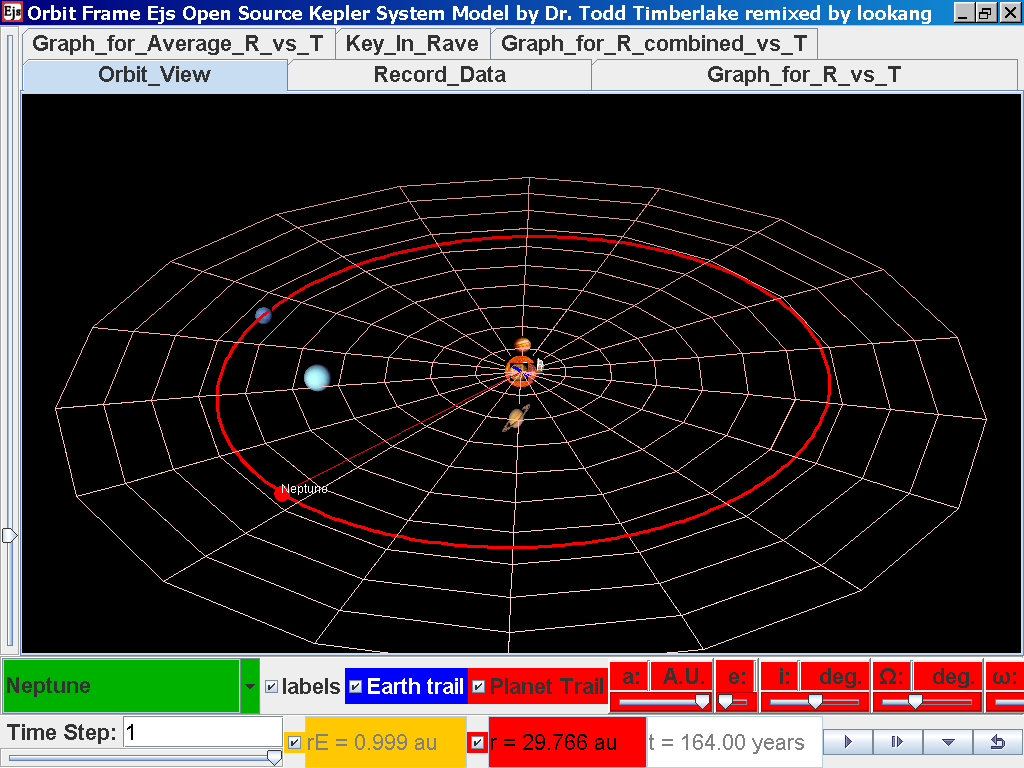
again click on the next tab Record_Data and select Record_Data. 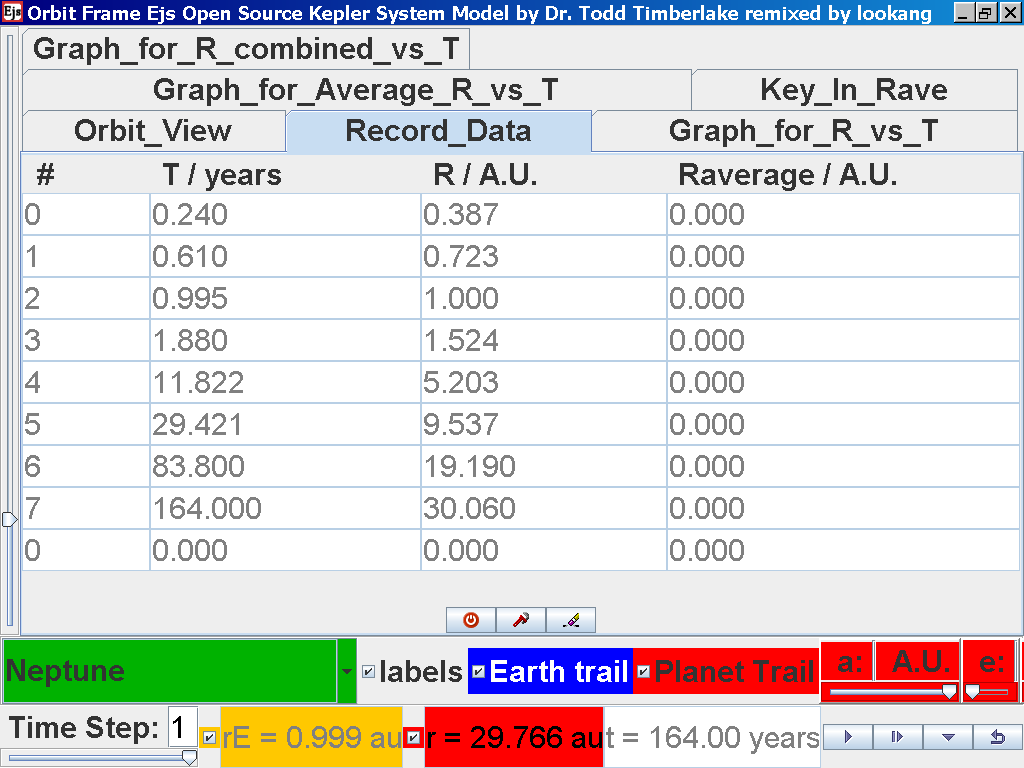
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Pluto. Play the simulation for one complete cycle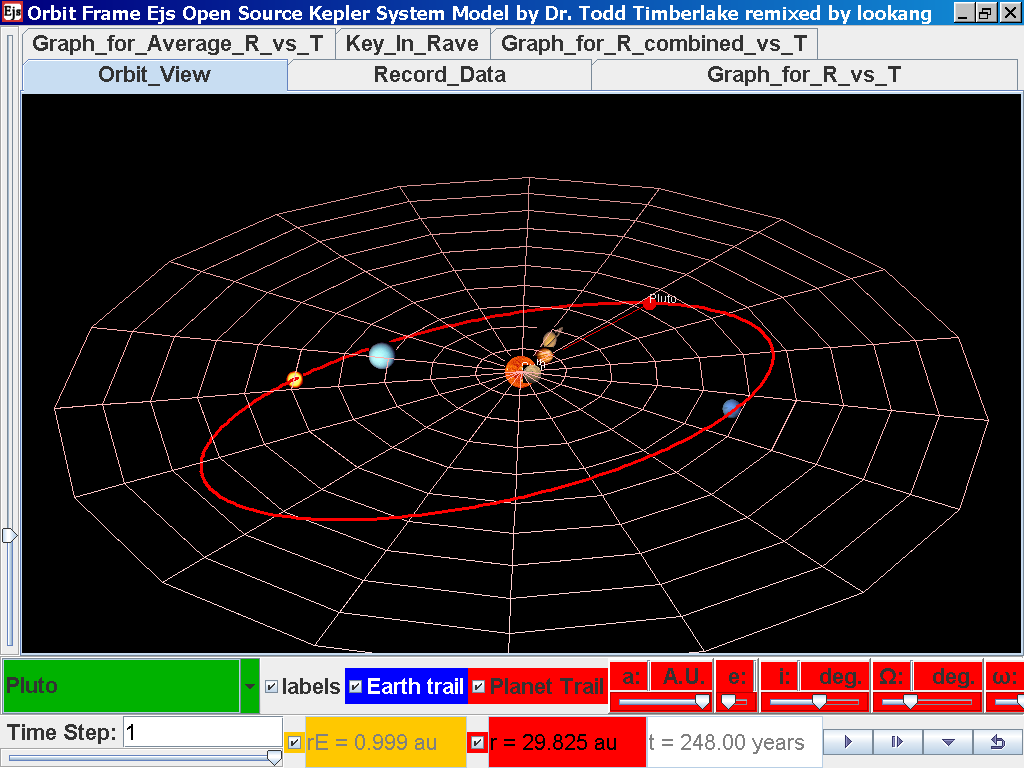
again click on the next tab Record_Data and select Record_Data. 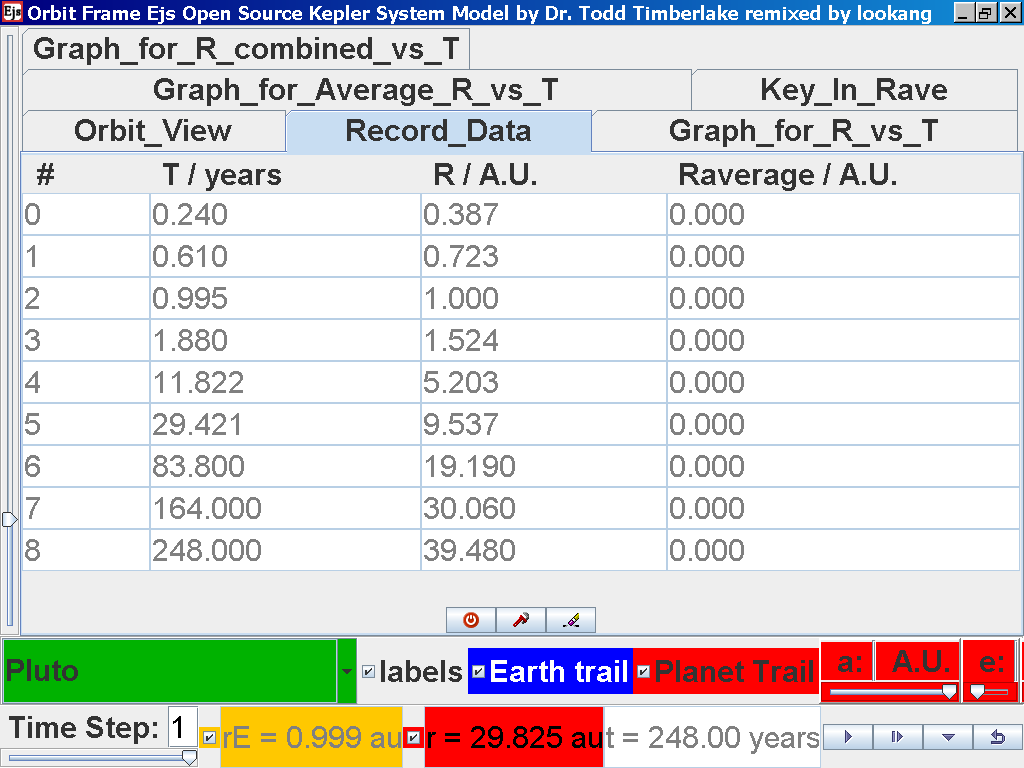
Notice all the data on the actual T /years recorded by you is slightly different and the mean radius of orbits R / A.U. astronomical units which 1 A.U. = mean distance of Earth to Sun.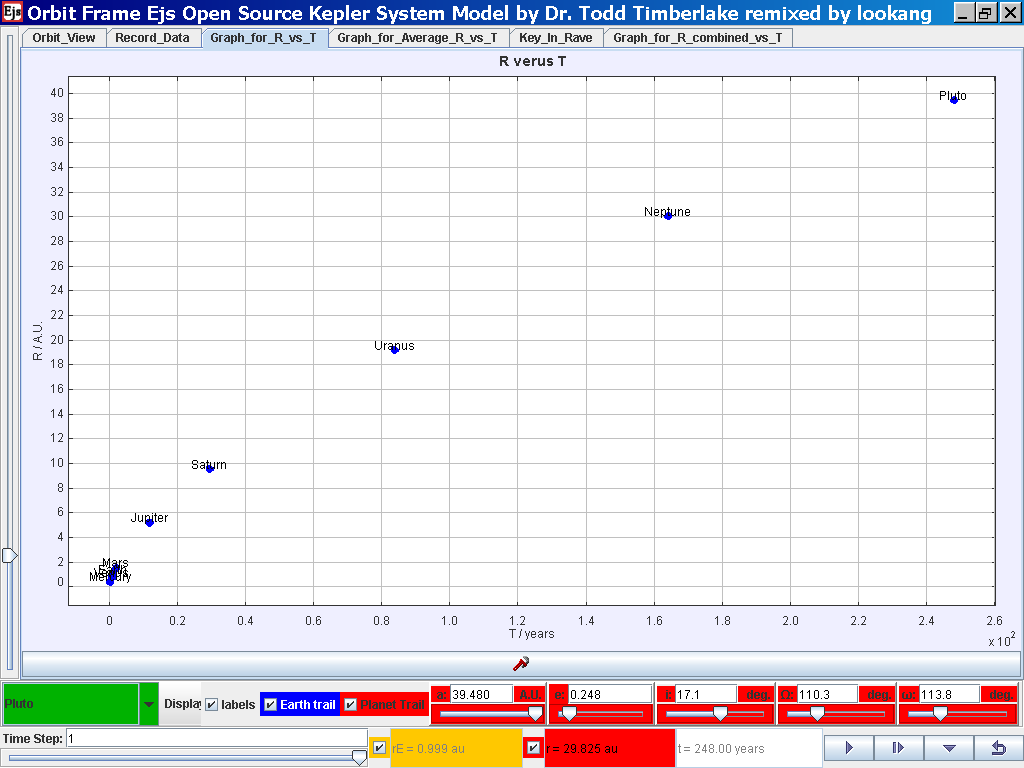
Select the tab Graph_for_R_vs_T and the simulation automatically plots the data.
Click on the Data Analysis Tool to bring up the following pop up view for further trend fitting.
Select the Data Builder Button at the top right corner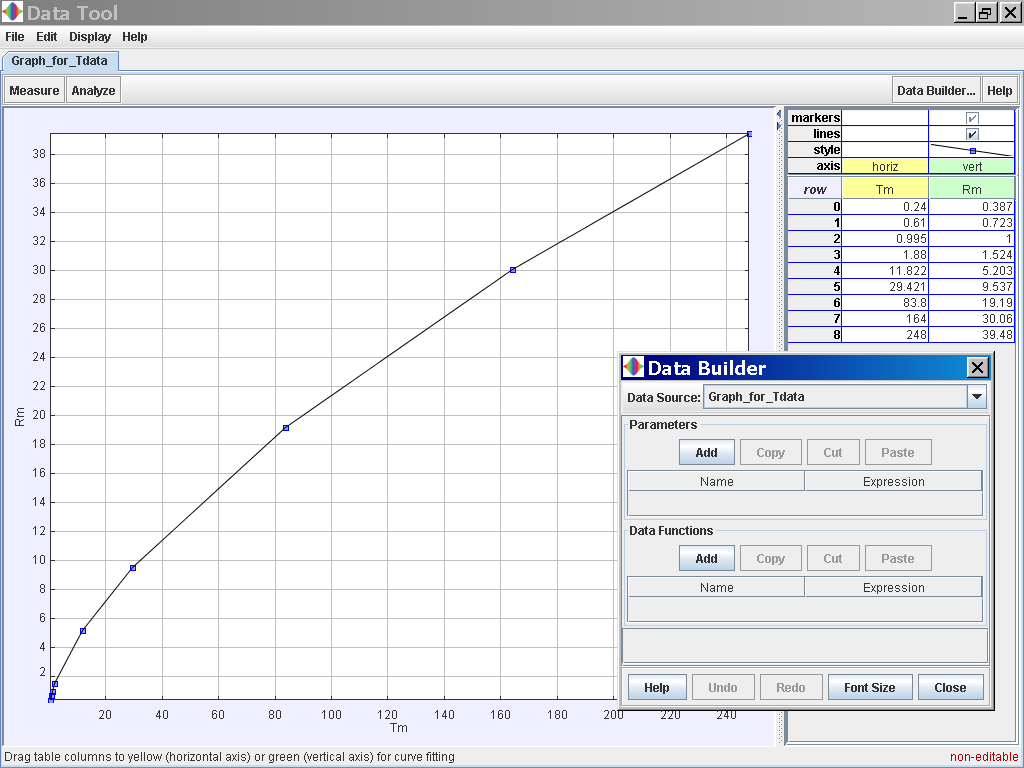
Click on the Data Function Add button to add your own functions such as T2 for Tmean2 and r3 for rmean3.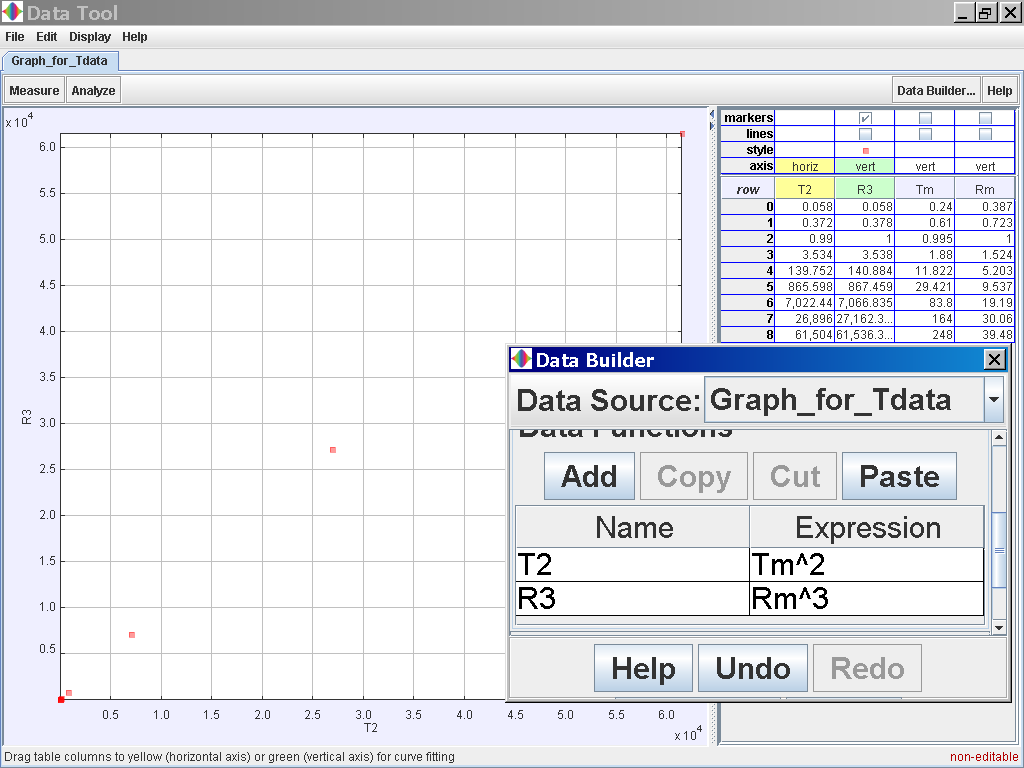 Click on the Analyse button on the top left corner and select the Linear Fit option of which the data of T2and R3 is related by the following line fit
Click on the Analyse button on the top left corner and select the Linear Fit option of which the data of T2and R3 is related by the following line fit
T2 = 0.998 R3 -20.753 which suggests T2 α r3
Alternative activity, you can also try to log (T) versus log (R)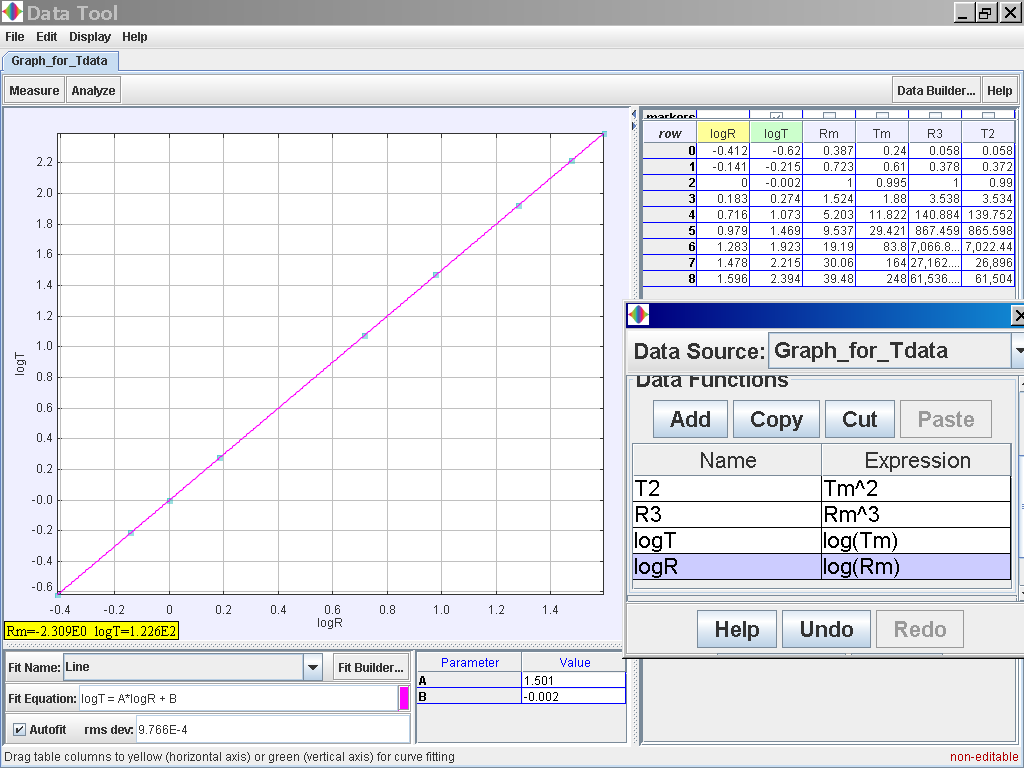 notice again log (T) = 1.501 log (R) -0.002 which suggests the same relationship of T α r1.5 or simply T2α r3
notice again log (T) = 1.501 log (R) -0.002 which suggests the same relationship of T α r1.5 or simply T2α r3
Youtube
Java Model
https://m.youtube.com/watch?utm_content=bufferc38b5&utm_campaign=buffer&utm_medium=social&v=zR3Igc3Rhfg&utm_source=twitter.com
Other resources
http://physics.weber.edu/amiri/director-dcrversion/newversion/kepler/Kepler_1.2.html
Versions
- http://weelookang.blogspot.sg/2016/07/75-keplers-solar-systemjavascript-html5.html
- http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_KeplerSystem3rdLaw09.jar
Worksheets
- IJC 2013 EJS Grav Worksheet 1 (Geostationary satellite, Kepler model) Student.docx
- IJC 2013 EJS Grav Worksheet 1 (Geostationary satellite, Kepler model).docx
- IJC 2013 EJS Grav Worksheet 2 (Gravitational field strength & potential ) Student.docx
- IJC 2013 EJS Grav Worksheet 2 (Gravitational field strength & potential ).docx
- IJC2013 H2T7 Gravitational Field Lect Notes (Teachercopy).docx
- IJC2013 Tut 7 Gravitational Field Tutorial (Q and A).docx
- IJC2013 Tut 7 Gravitational Field Tutorial (Q only).docx
- IJC2013_H2T7_Gravitational_Field_Lect_Notes_(Teachercopy) edited.docx
- IJC2013_H2T7_Gravitational_Field_Lect_Notes_(with Solutions).pdf
- IJCCheat Sheet Gravitation.docx
- IJCExcel for Kepler.xlsx
- IJCH2_AFL_Gravitation_2013_(teacher)_edited.docx
- IJCTopic 7 H2 Gravitational Field 2013 (Part1).pptx
- YJC2013 H2 Phy Topic 7 Gravitational field - ICT inquiry worksheet 1 on Field strength & Potential (Teacher).doc
- YJC2013 H2 Phy Topic 7 Gravitational field - ICT inquiry worksheet 2 on Kepler's Third Law (Teacher).doc
- YJC2013 H2 Phy Topic 7 Gravitational field - ICT inquiry worksheet 3 on Geostationary satellite (Teacher).doc
- YJC2013 H2 Phy Topic 7 Gravitational field - Lect notes (Teacher).doc
- YJC2013 H2 Phy Topic 7 Gravitational field - Tutorial (Teacher).doc
- YJC2013Yishun JC H2 Physics - Gravitational field ICT inquiry worksheet 1 (For upload).doc
- YJC2013Yishun JC H2 Physics - Gravitational field ICT inquiry worksheet 2 (For upload).doc
- YJC2013Yishun JC H2 Physics - Gravitational field ICT inquiry worksheet 3 (For upload).doc
- YJC2013Yishun JC H2 Physics - Gravitational field Lecture notes (For upload).pdf
- YJC2013Yishun JC H2 Physics - Gravitational field Powerpoint Slides (For upload).pdf
- YJC2013Yisun JC H2 Physics - Gravitational field Tutorial (For upload).doc
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Loo Kang Wee
- Parent Category: 02 Newtonian Mechanics
- Category: 08 Gravity
- Hits: 12482