About
7.3.8.6 Example of Application of potential ϕ
7.3.8.6.1 Revision:
The total ϕ at a point in a field due to two or more source masses is the scalar addition of the individual ϕ due to each mass at that point, i.e. .
ϕtotal = ∑ϕ
Similarly, since PE = U = mϕ
PE total =
Showing how the gravitational potential varies between the surface of the Moon and the surface of the Earth along the line joining the centres.
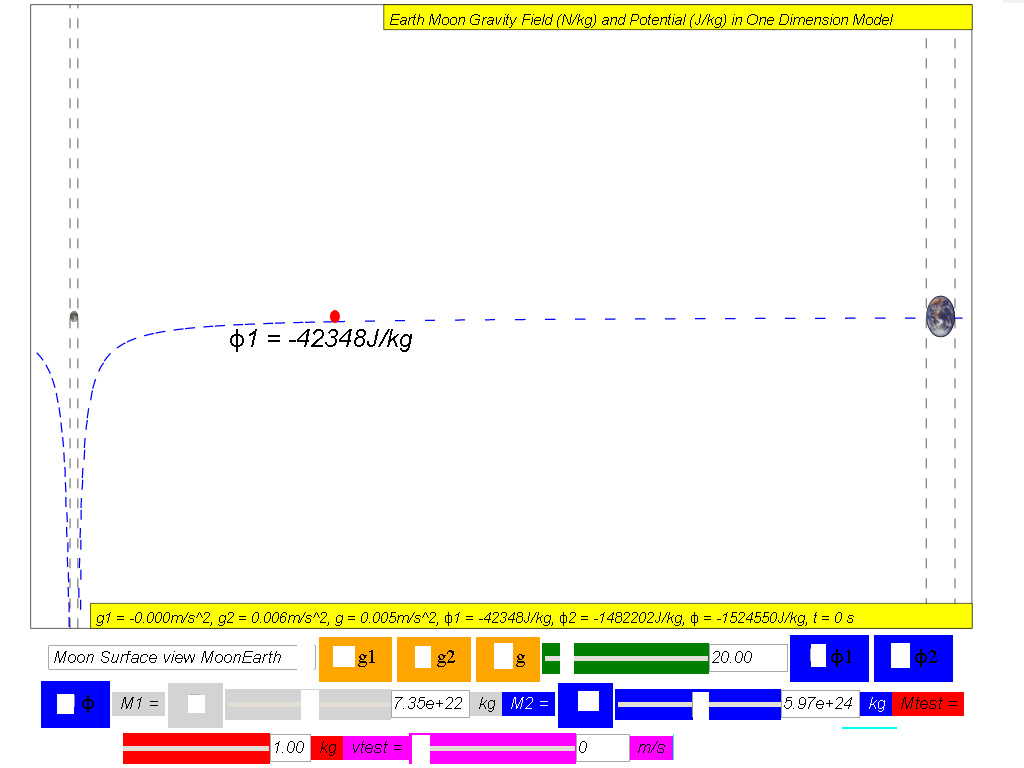
ϕ1 = Gravitational potential due to Moon
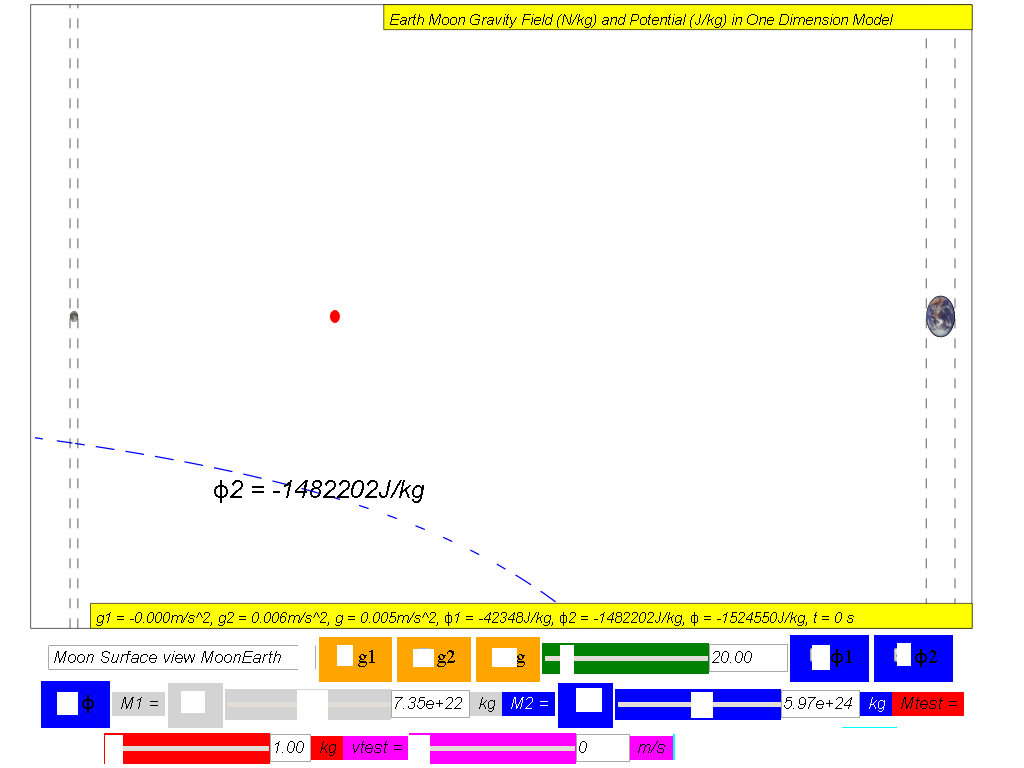 ϕ2 = Gravitational potential due to Earth
ϕ2 = Gravitational potential due to Earth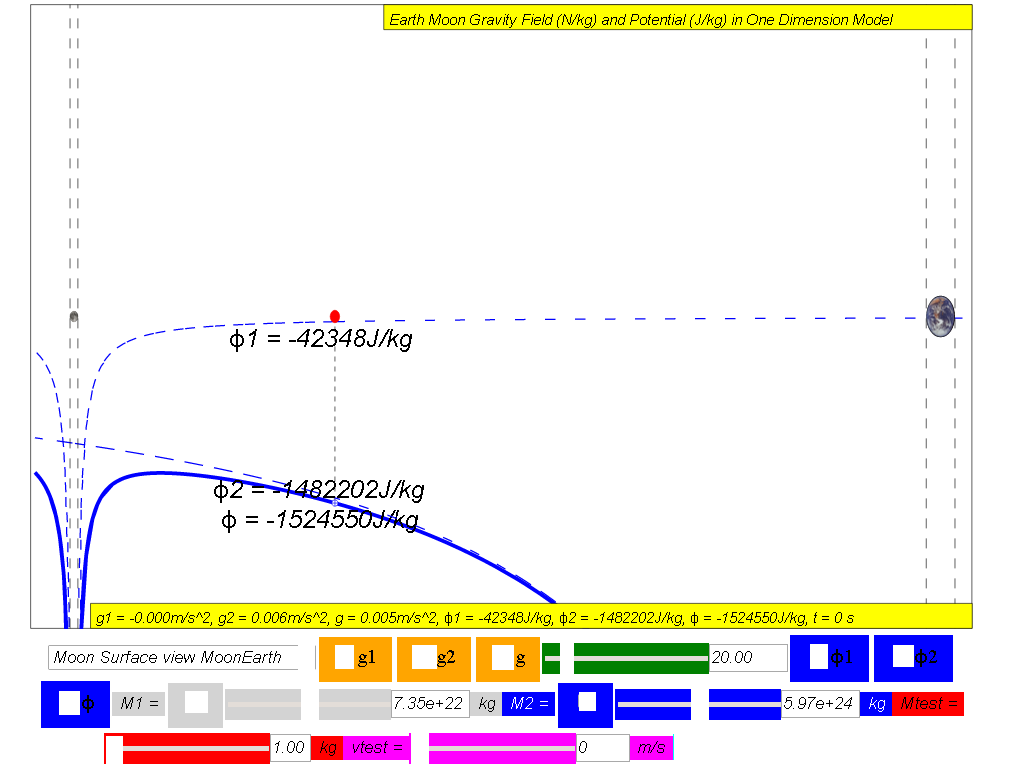
ϕtotal = ϕ1 +ϕ2 = Net gravitational potential along the line of centres is equal to the sum of the gravitational potentials due to the Earth and Moon
7.3.8.6.2 Escape Speed Is it true that 'what goes up must come down'?
It is only accurate to say that 'what goes up may come down'. There is a critical speed at which an object can be launched such that it can escape the Earth permanently. Such a critical speed is termed as the escape speed.7.3.8.6.2.1 Example Determine an expression for the escape speed, v, of a rocket of mass m launched from the surface of Earth of mass M and radius R.
By conservation of energy, assuming at r = ∞, the minimum speed is 0.
KEearth surface + PEearth surface = KE∞ + PE∞
v = 1.12x104 m/s
Therefore, to escape from Earth, it implies that the projectile must have a minimum launch velocity of v = 1.12x104 m/s .
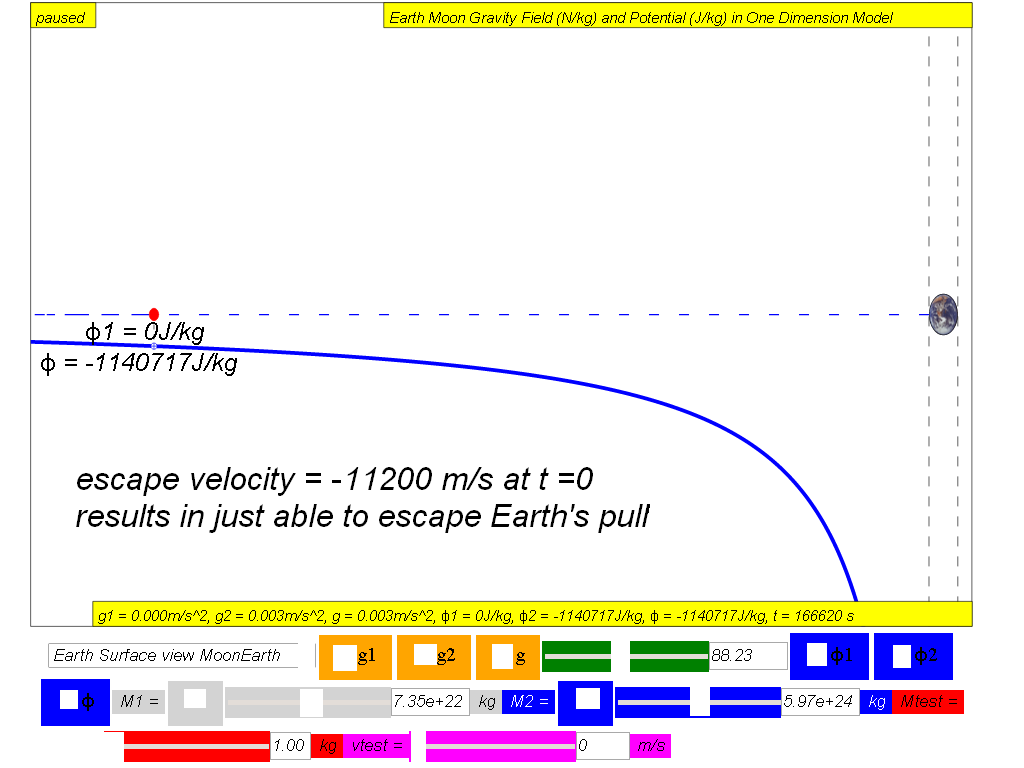
To understand the escape velocity concept, the following steps could be used as an inquiry approach to experience escape velocity in the context of the simulation.
- Un-check the M1 moon to remove the effects of the Moon
- Select from the drop-box menu the option Earth Surface view MoonEarth (Left to Right), and notice the test mass (red) is placed on the surface of the Earth on the right side.
- Key in on the vtest, velocity of the test mass (magenta) say -10000 m/s (negative as the velocity points to the left of the Cartesian coordinate system)), and click play to observe the effects of launching a projectile at this speed. You could record your observation as "unable to escape from Earth's gravity pull.

Similarly, design an experiment to discover the minimum theoretical speed to escape from Earth's pull.
Can you conclude that any velocity lesser than v = 1.12x104 m/s cannot allow the projectile to escape from Earth's pull?
Can you conclude that any velocity greater than vescape Earth = 1.12x104 m/s allow the projectile to escape from Earth's pull?
Similarly, you can derive the theoretical escape velocity from Earth's Moon surface and test it on the simulation.
Answer: vescape Moon=2400 m/s
Given that root-mean-square speed is the measure of the speed of particles in a gas that is most convenient for problem solving within the kinetic theory of gases, is given by
Given molar gas constant R = 8.31 J K−1 mol−1, molar mass of water is Mm H20 = 18x10-3 kg/mol , T is temperature in Kelvin, using the minimum theoretical speed from Moon, suggest the surface temperature of Moon at some point in its history which resulted in the Moon's surface not having water now.
T = 4.2x103 K
With this limited information, this data seems to suggest at some point of Moon's history, it could have been very hot (T = 4.2x103 K) which causes water molecules to escape then. As the Moon cools, not enough water molecules was able to form on the Moon's surface to form oceans like what we have on Earth.
7.3.8.6.3 Model ϕ
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); andrew duffy
lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); andrew duffy
Versions:
- http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GFieldandPotential1Dv7EarthMoon.jar by Todd TimberLake and lookang Java version
Other resources
https://www.geogebra.org/m/va3dbqyd by Seng kwang
Writeup ICT
Virtual Laboratory Gravitational Field & Potential of Earth and Moon
Students will be able to:
1) recall and apply the equation g = GM/r^2 for the gravitational field strength of a point mass to new situations or to solve related problems; and
2) solve problems using the equation φ = -GM/r for the potential in the field of a point mass.
1) recall and apply the equation g = GM/r^2 for the gravitational field strength of a point mass to new situations or to solve related problems; and
2) solve problems using the equation φ = -GM/r for the potential in the field of a point mass.
The lesson was tested & carried out with JC1 as a research on physics by inquiry using simulations.
ICT equipments used included Computers, with Java Runtime installed, Ejs Open Source Gravitational Field & Potential of Earth and Moon Java Applet 2mb file copied into the desktop.
Full screen applet
Author: Andrew Duffy and lookang
Pedagogy is active learner centered learning with technology (simulation).
Strategies Teacher as technology, content, pedagogy and knowledge expert (TPCK), facilitating the inquiry learning process, with teacher to facilitate at suitable times.
Thinking skills, Self directed planning of inquiry approach is required for students to collect data, Science Practical Assessment Skill A. Analysis of data skill is also practiced. Evaluation of data and finally Synthesis skill during the proposing and verifying of their hypothesis of the physics principle .
Lesson is 1 hour 40 mins and some home based learning as students are equipped with computer 1 to 1 access as a pilot study on 1 to 1 computing access.
ICT equipments used included Computers, with Java Runtime installed, Ejs Open Source Gravitational Field & Potential of Earth and Moon Java Applet 2mb file copied into the desktop.
Full screen applet
Author: Andrew Duffy and lookang
Pedagogy is active learner centered learning with technology (simulation).
Strategies Teacher as technology, content, pedagogy and knowledge expert (TPCK), facilitating the inquiry learning process, with teacher to facilitate at suitable times.
Thinking skills, Self directed planning of inquiry approach is required for students to collect data, Science Practical Assessment Skill A. Analysis of data skill is also practiced. Evaluation of data and finally Synthesis skill during the proposing and verifying of their hypothesis of the physics principle .
Lesson is 1 hour 40 mins and some home based learning as students are equipped with computer 1 to 1 access as a pilot study on 1 to 1 computing access.
Students work were captured in the worksheet.
2011
Gravitational Fields
Simulations
EN
Post-Sec
EO
Goh Giam Hwee / Yishun Junior College
Goh Giam Hwee /Yishun Junior College
Wee Loo Kang/ This email address is being protected from spambots. You need JavaScript enabled to view it./ Educational Technology Division
Resources
https://www.geogebra.org/m/va3dbqyd by Tan Seng Kwang
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 08 Gravity
- Hits: 11881


.png
)





