About
1.2.4 Acceleration
From v = vo cos ω t = x0 ω cos ω t
where xo is the maximum displacement
differentiating we get
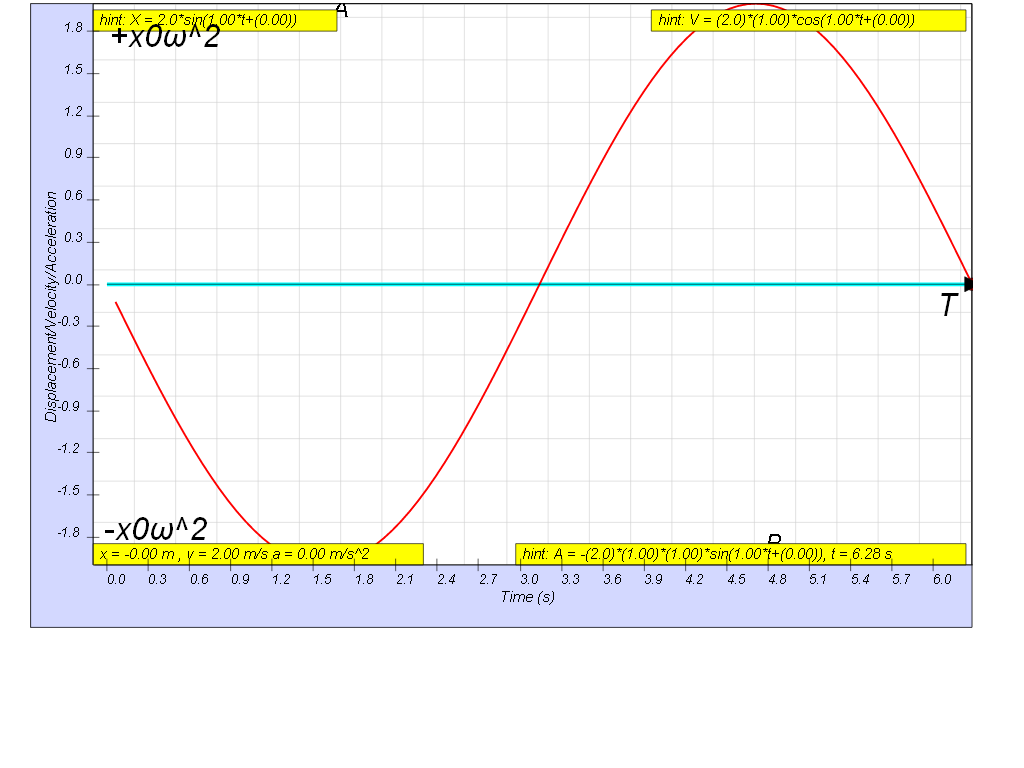
Variation with time of acceleration
In terms of x:
Therefore, a = - xo ω2 sin ω t
= - ω2 (xo sin ω t)
which is the defining equation for S.H.M. !
a = - ω2 x
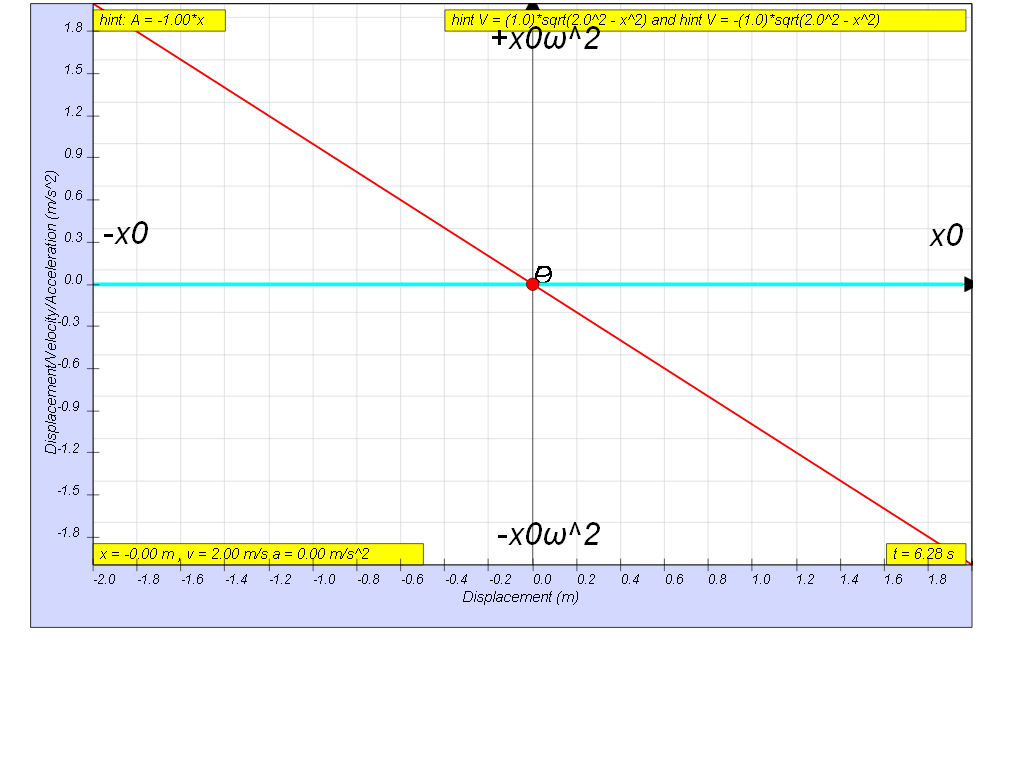
Variation with displacement of acceleration
since
a = – a0sin ω t
where ao is the maximum acceleration
where by a0 = ω2 (xo)
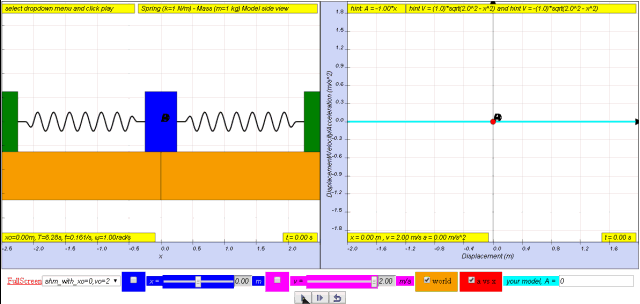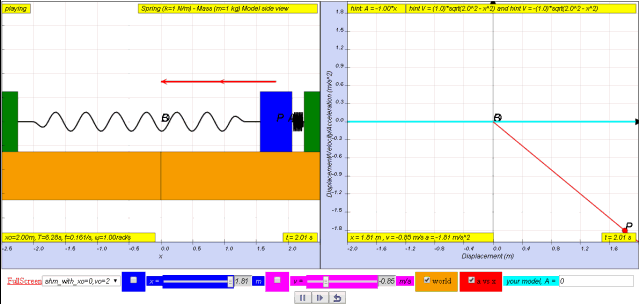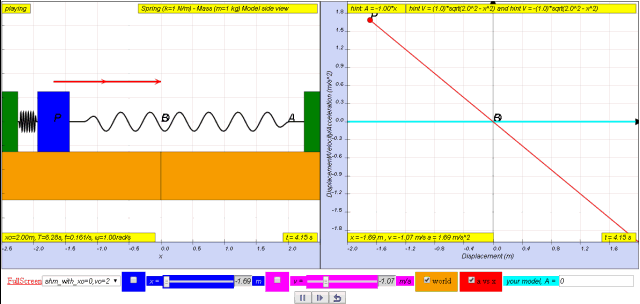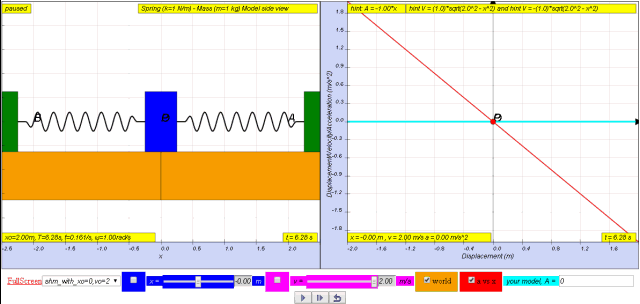
1.2.3.1 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 5902








