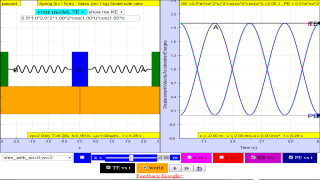
About

1.3 a)    Variation with time of energy in simple harmonic motion

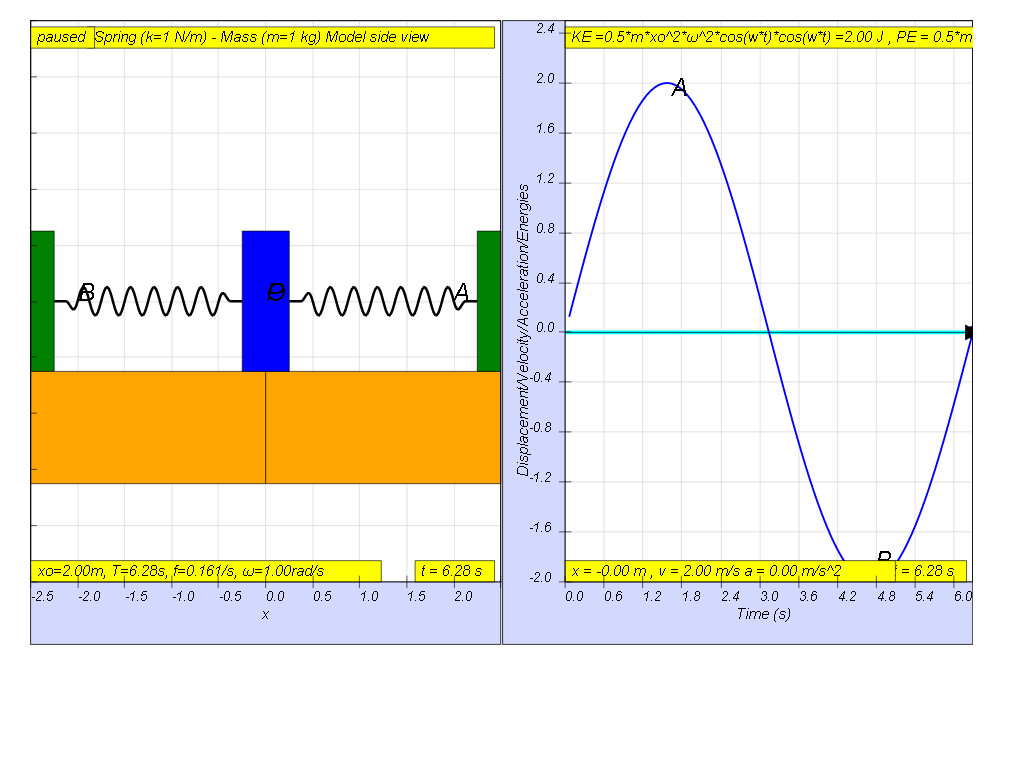
If the variation with time of displacement is as shown, then the energies should be drawn as shown.


recalling Energy formula

KE = ½ m v²

PE =  ½ k x²

in terms of time t,

x = x₀ sin(ωt) 

differentiating with t gives

v = v₀ cos (ωt)

therefore, KE = ½ m v²= ½ m (v₀ cos (ωt))²= ½ m (x₀²ω²)cos (ωt))²

similarly

PE = ½ k x²= ½ (mω² )(x₀ sin (ωt))²= ½ m (x₀²ω² )sin (ωt))²

therefore total energy is a constant value in the absence of energy loss due to drag (resistance)

TE = KE + PE = ½ m (x₀²ω² )[cos²(ωt) + sin²(ωt))] = ½ m (x₀²ω²)

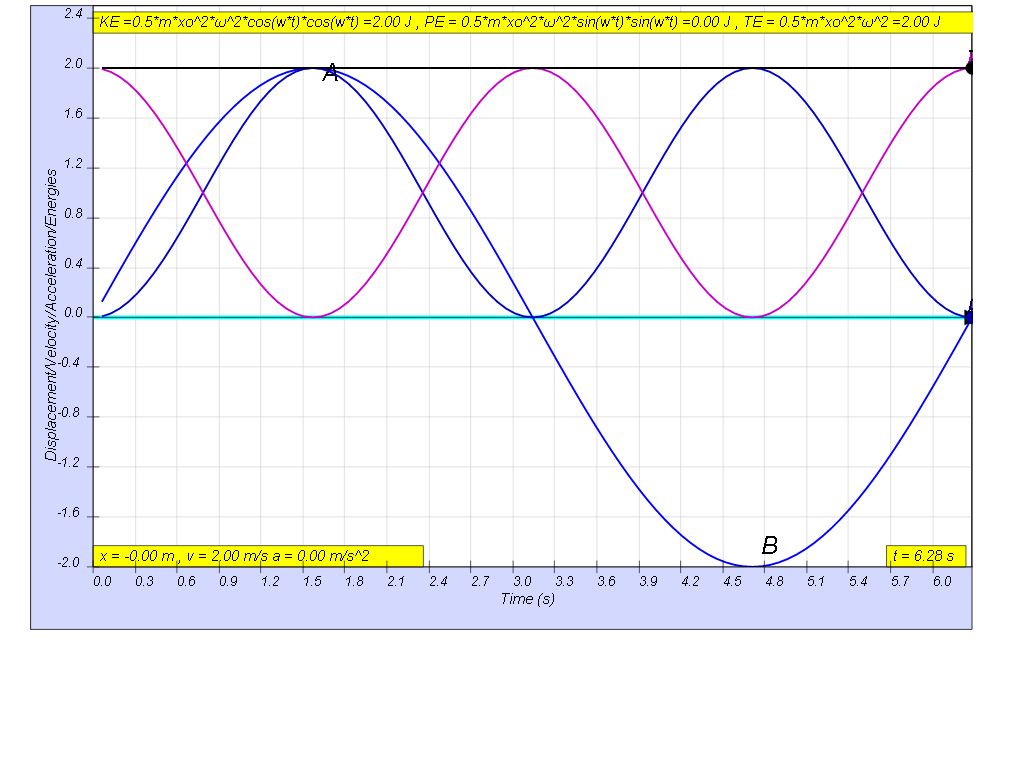
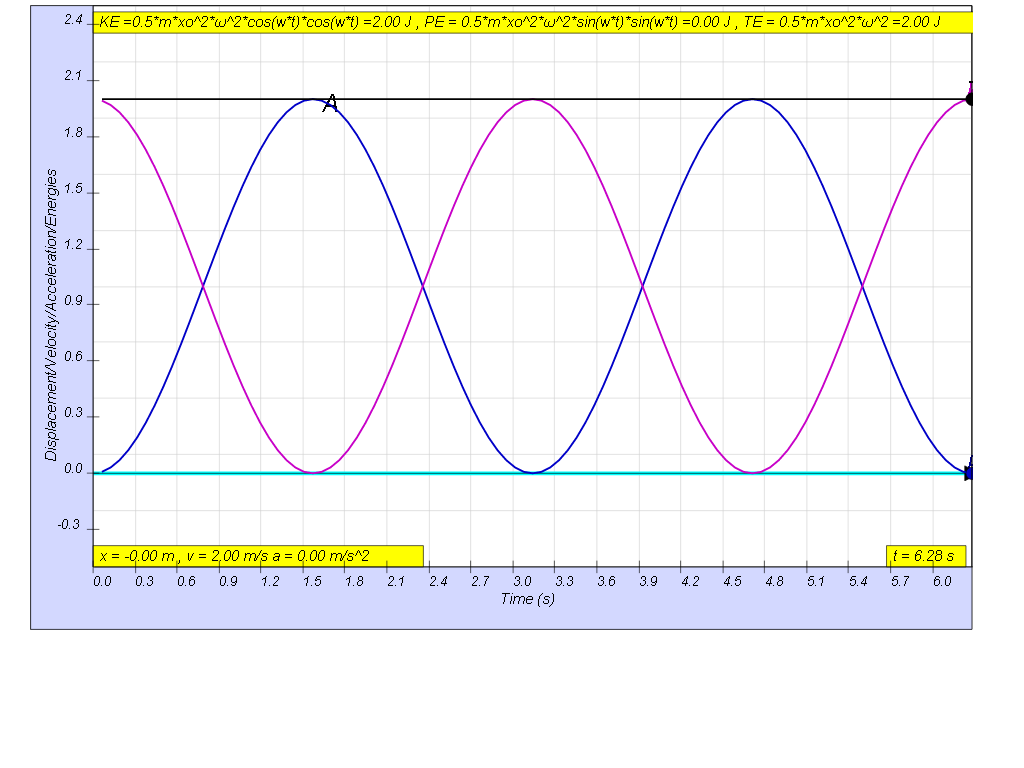
this is how the x vs t looks together of the energy vs t graphs

1.3.1 Summary

the table shows some of the common values

general energy formula	SHM energy formula	when t = 0	when t = T/4	when t = T/2	when t = 3T/4	when t = T
KE = ½ m v2	½ m (x02ω2)cos (ωt))2	½ m (x02ω2)	0	½ m (x02ω2)	0	½ m (x02ω2)
PE =  ½ k x2	½ m (x02ω2)cos (ωt))2	0	½ m (x02ω2)	0	½ m (x02ω2)	0
TE = KE + PE	TE = ½ m (x02ω2)	½ m (x02ω2)	½ m (x02ω2)	½ m (x02ω2)	½ m (x02ω2)	½ m (x02ω2)

1.3.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/80

 

Translations

Code	Language		Translator	Run

Software Requirements

	Android	iOS	Windows	MacOS
with best with	Chrome	Chrome	Chrome	Chrome
support full-screen?	Yes. Chrome/Opera No. Firefox/ Samsung Internet	Not yet	Yes	Yes
cannot work on	some mobile browser that don't understand JavaScript such as.....		cannot work on Internet Explorer 9 and below

 

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

end faq