About
Topics
TransverseDescription
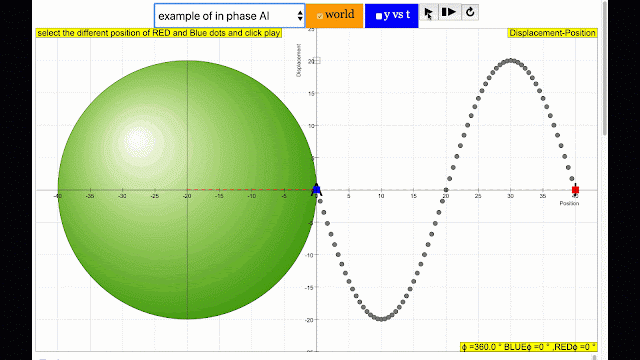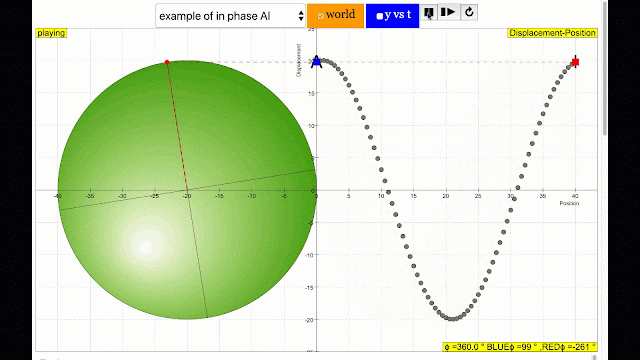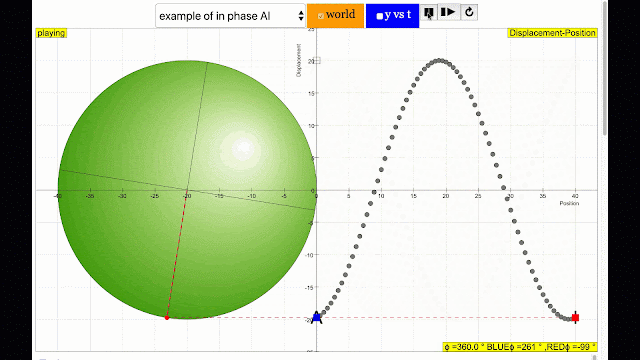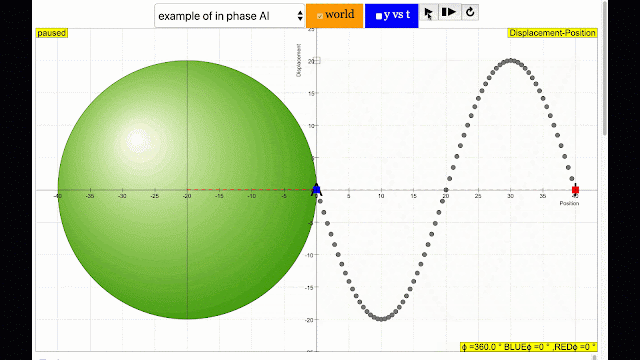
In this Transverse wave model, the simulation shows the phase difference commonly associated in wave motion in terms of angle differences between the 2 points travelling in a circular motion.Sample Learning Goals
(a) show an understanding and use the terms displacement, amplitude, phase difference, period,frequency, wavelength and speed
(f) analyse and interpret graphical representations of transverse
Activities
- By changing i and j sliders, the different positions of a wave can be simulated.
- Determine the phase difference between the BLUE and RED point using ϕ/(2π) = t/T or otherwise.
- Use the simulation to check your calculation.
- The slider T changes the period of the wave motion, by means of evidences from the simulation or otherwise, determine the period
- The slider A changes the amplitude of the wave motion, by means of evidences from the simulation or otherwise, determine the amplitude
- the guide allows the visualization of the front view of the point BLUE and RED.
Version:
- http://weelookang.blogspot.sg/2015/07/ejss-transverse-wave-model.html
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_waves_leetl_wee_v6.jar
http://weelookang.blogspot.sg/2015/07/ejss-transverse-wave-model.html
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits

 Lee Tat Leong; Wee Loo Kang
Lee Tat Leong; Wee Loo Kang
Description
Phase is the position of a point in time (an instant) on a waveform cycle. A complete cycle is defined as the interval required for the waveform to return to its arbitrary initial value. The graph to the right shows how one cycle constitutes 360° of phase.
|
phase difference equal to zero also called in phase. notice point A and I are moving up and down the wave where their projected position on the circle form 0 degree difference, thus called in phase. |
|
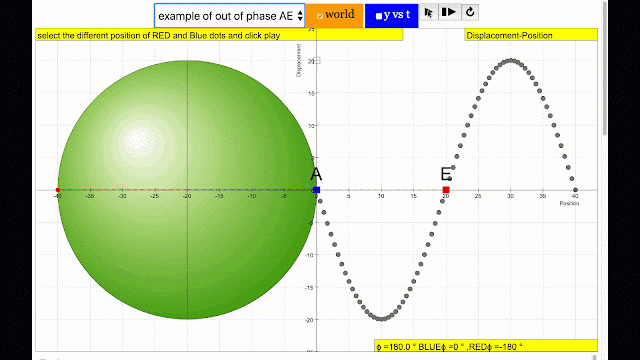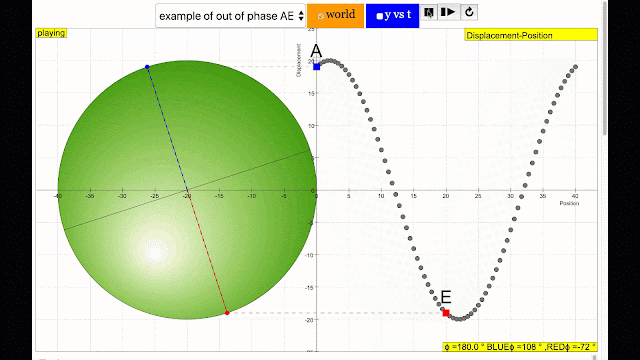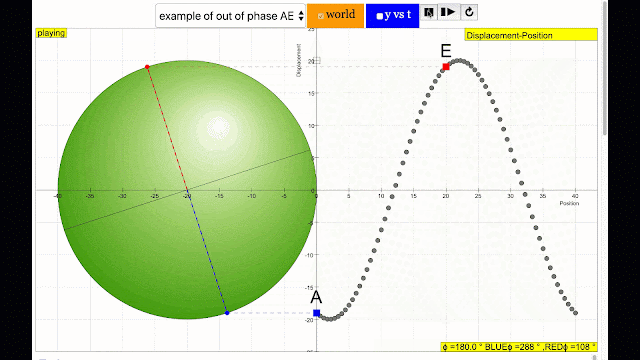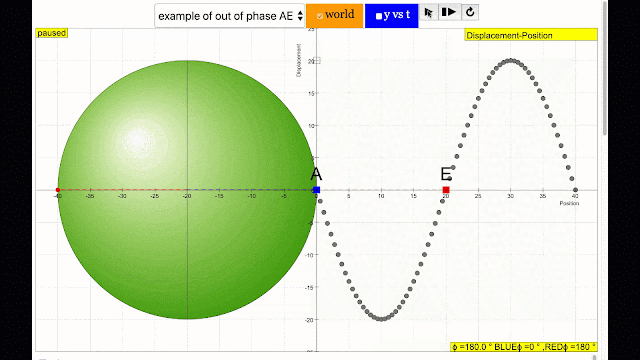
phase difference equal to 180 degrees also called antiphase. notice point A and E are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees. |
|
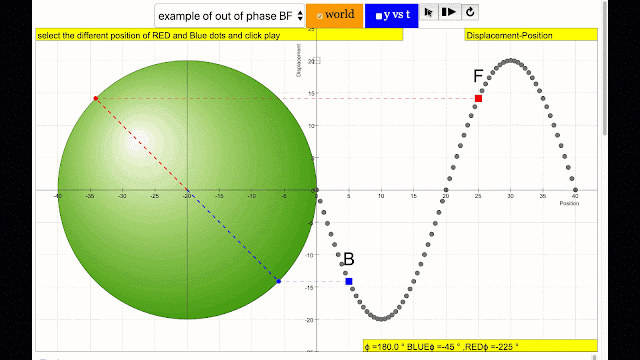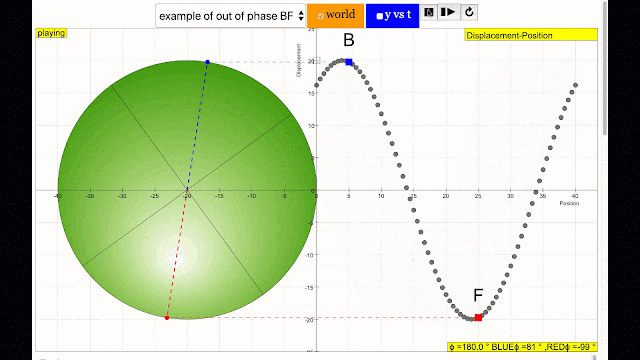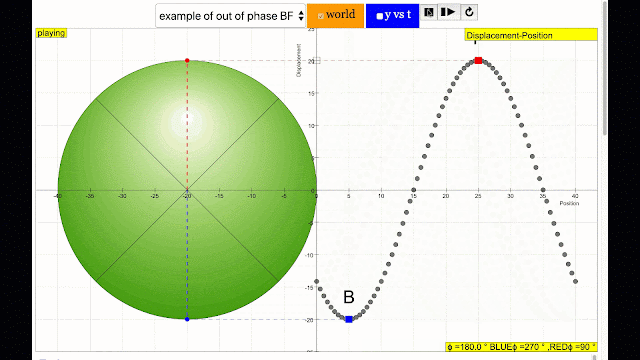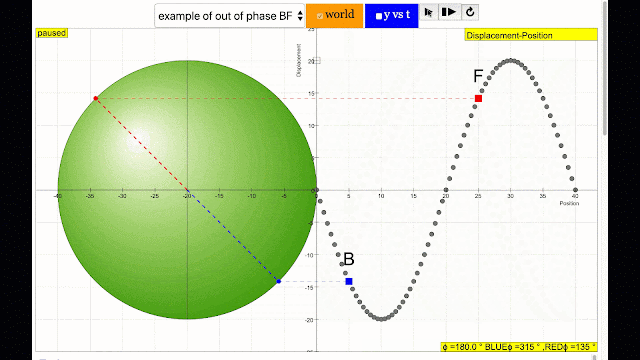
phase difference equal to 180 degrees also called antiphase. notice point B and F are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees. |
|
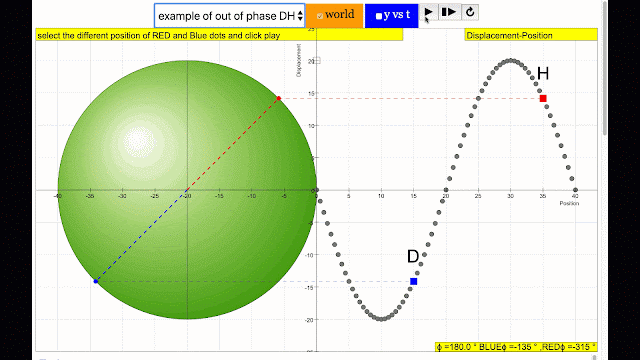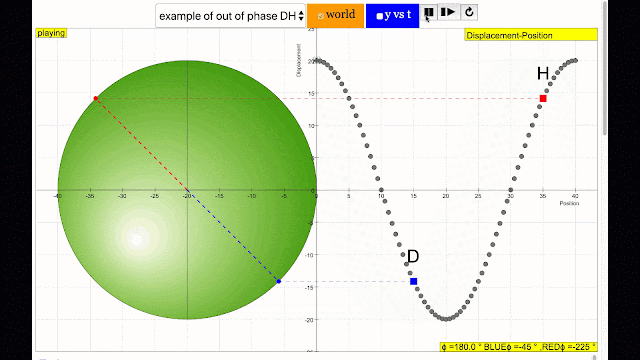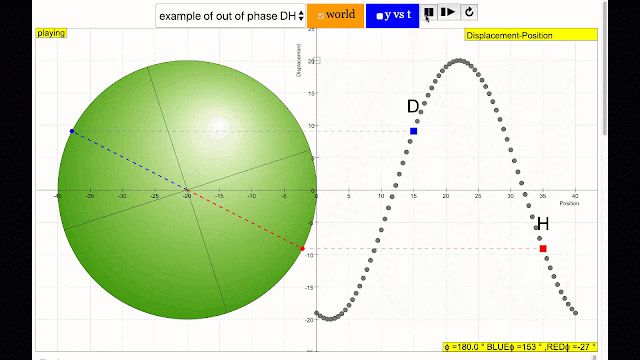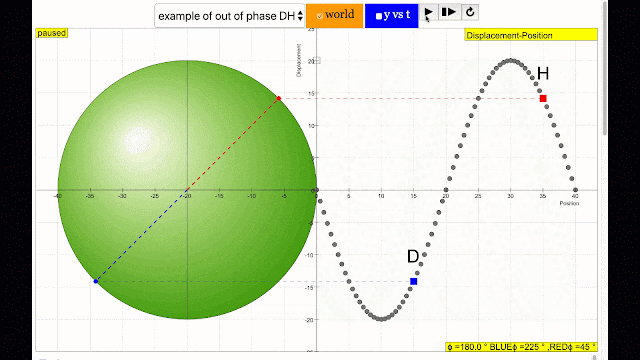
phase difference equal to 180 degrees also called antiphase. notice point D and H are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees. |
|
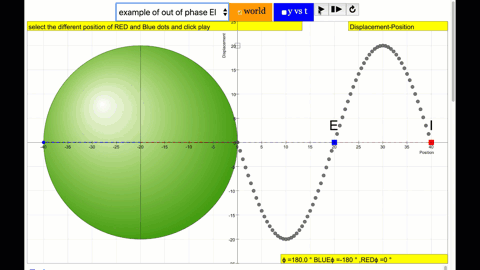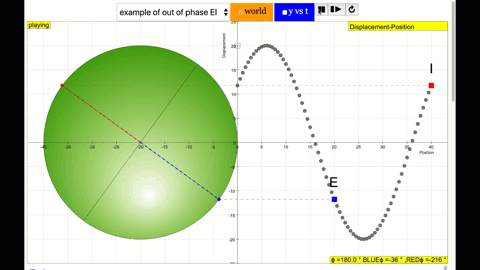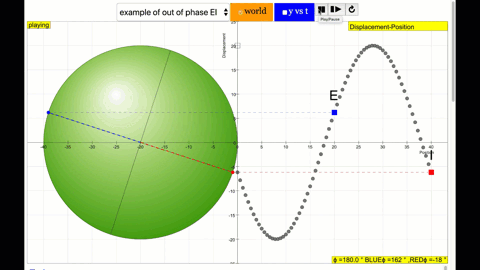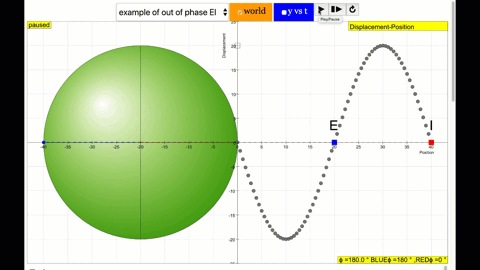
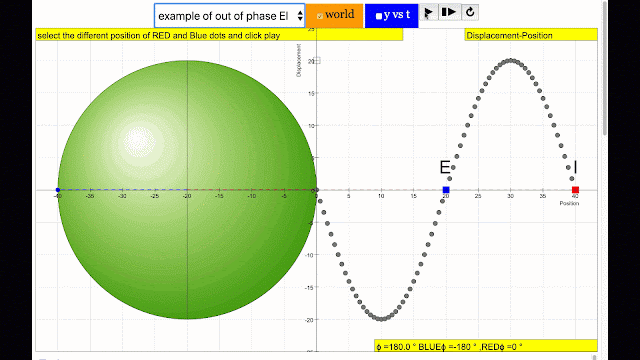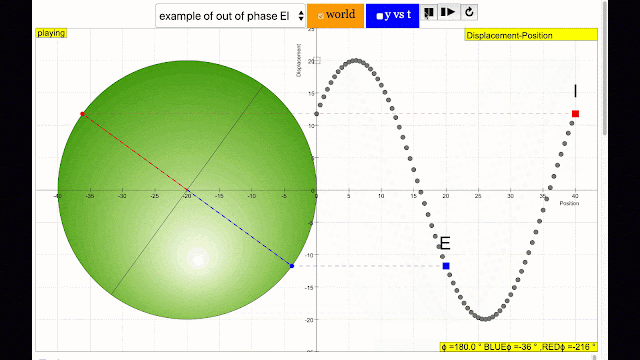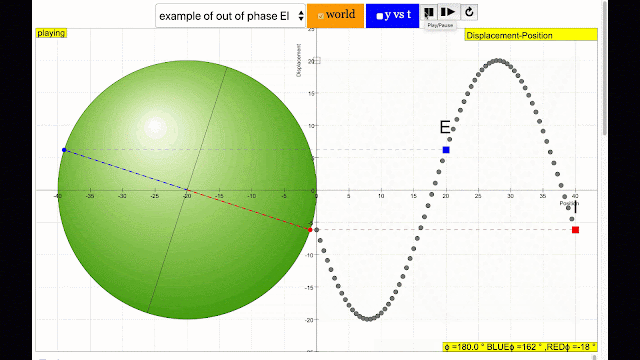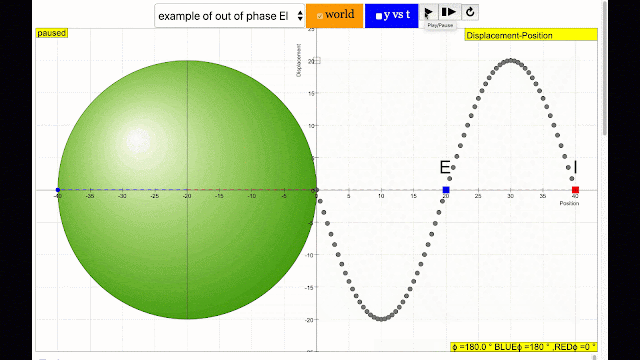
phase difference equal to 180 degrees also called antiphase. notice point E and I are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees. |
|
phase difference equal to 180 degrees also called antiphase. notice point E and I are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees. |
|
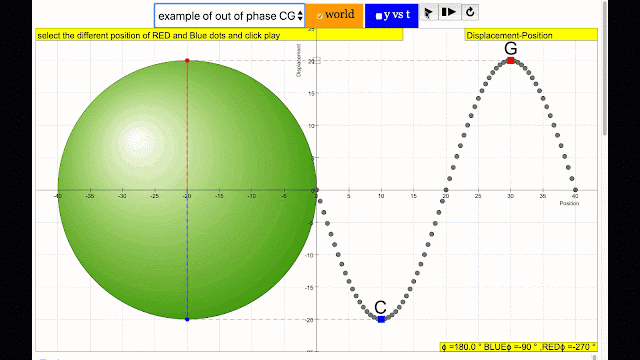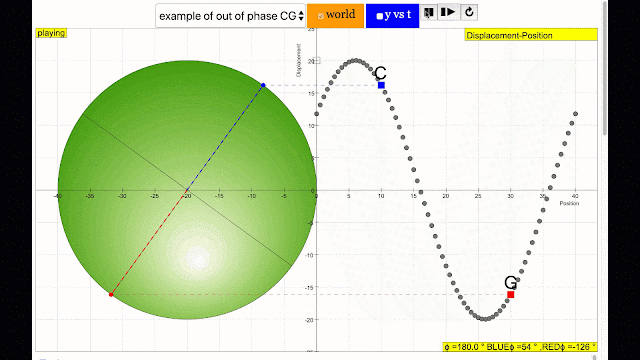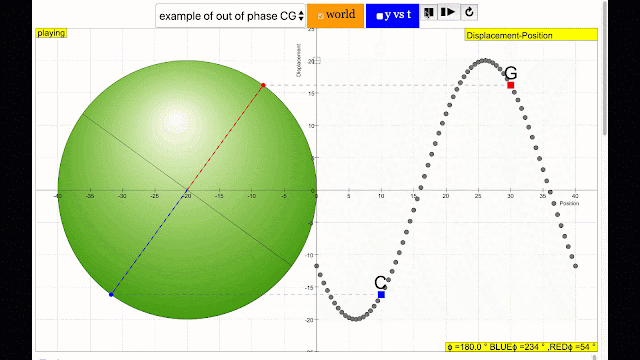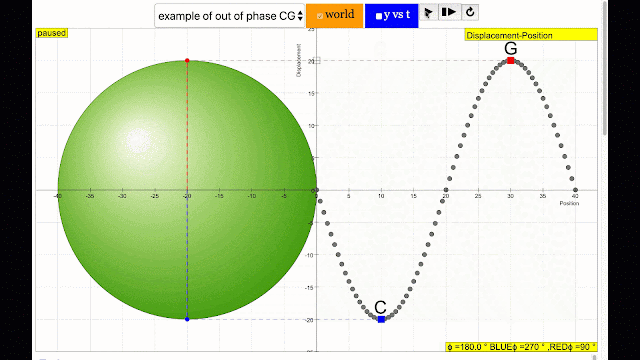
phase difference equal to 180 degrees also called antiphase. notice point C and G are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees. |
Video
Versions
http://weelookang.blogspot.com/2019/01/transverse-phase-difference-wave.html
Phase Difference
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Parent Category: 03 Waves
- Category: 01 General Waves
- Hits: 15208


.png
)