About
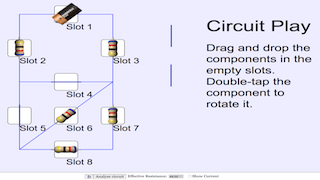
Circuit Play
- Drag and drop the wires, cell and 24 Ohm resistors into the empty slots.
- Double-tap to rotate the component.
- Analyze the circuit to get the effective resistance.
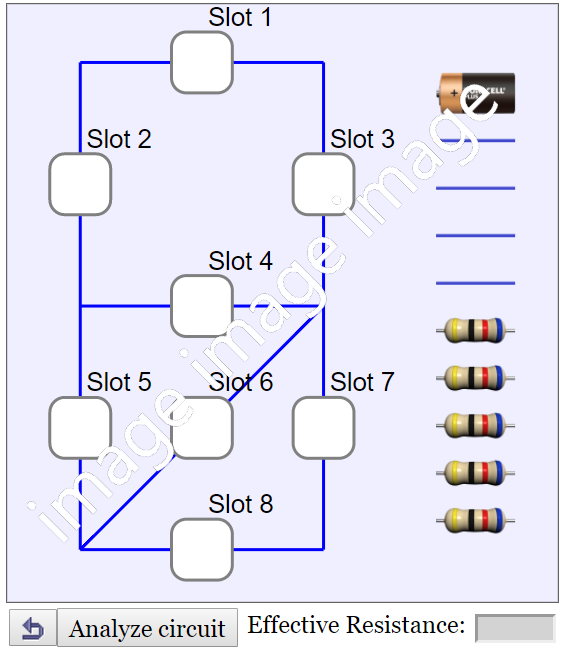
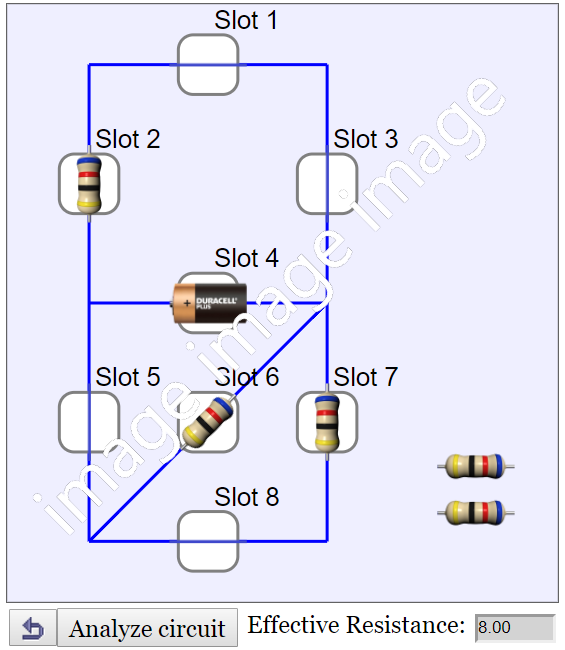
This is a simulation of a simple direct current (D.C.) circuit. By putting wires and resistors at the slots, the effective resistance of the circuit can be analysed and calculated. There are a total of 8 slots to be connected with a choice of 10 components including one battery, four wires and five resistors.
The resistance in the battery and the wires is assumed to be zero ohm.
In order to connect the components correctly, double-tap a component to change its orientation. Each double-tap will rotate the component 45 degree counterclockwise. A component's orentation affects its connection with the rest of the circuit.
The effective resistance of n resistors connected in series can be calculated using the following equation:
Reff = R1 + R2 + R3 + ... + Rn
The effective resistance of n resistors connected in parallel can be calculated using the following equation:
Reff = 1 / (1/R1 + 1/R2 + 1/R3 + ... + 1/Rn)
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 Francisco Esquembre; Kay Shin Tan
Francisco Esquembre; Kay Shin Tan
Alternate Concepts
- student believe that current is “used up” in a circuit, when in fact it is the electric potential that causes the flow of electrons, where electrons is always present in the wires.
- student believe the current through a battery will always have the same value, regardless of the number or configuration (series or parallel) of components in the circuit, when in fact current can vary according to the circuit connections.
- Students referred to current, voltage, energy, and power inappropriately and sometimes interchangeably.
- Failure to distinguish between voltage and current
- Failure to apply concept of complete circuit and current flow correctly
Version
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Fremont
- Parent Category: 05 Electricity and Magnetism
- Category: 05 Circuits
- Hits: 7770