About
7.3.8 Relationship between F and U; between g and ϕ
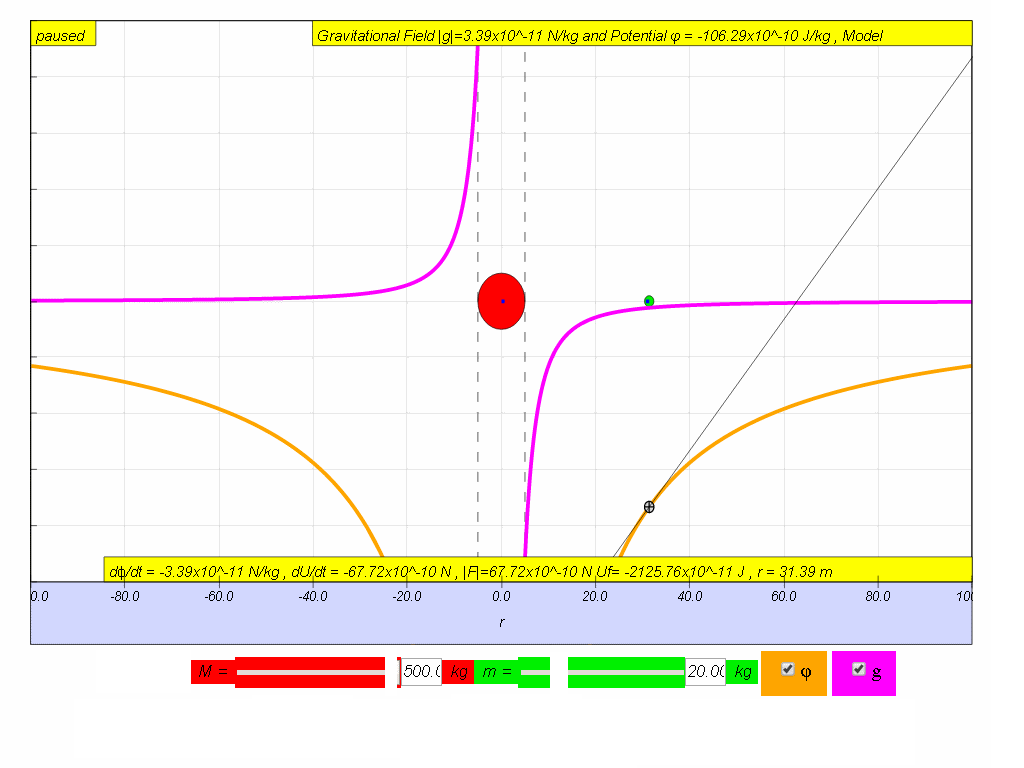
To understand how g is related to ϕ:
- Similarly, compare and in the above table.
- If we differentiate with respect to r, we will get , which has the same expression as g.
- Hence, mathematically
- To understand the meaning of observe the two graphs carefully, on the right side where r is positive, the gradient of ϕ vs r graph is positive but the value of g will be negative. And on the left side where r is negative, the gradient of ϕ vs r graph is negative but the value of g is positive. Thus,
Similarly, it can be concluded that by multiplying both sides by test mass m.
thus
7.3.8.1 Activity To do
ICT inquiry worksheet 1 (E), as well as the "G field and potential" EJS here. The HTML5 version is below, the Java worksheet customization to HTML5 is work in progress.7.3.8.2 Summary
| symbol | ||
| name | Field strength | Potential |
| units | N kg-1 or m s-2 | J kg-1 |
| meaning | Gravitational force per unit mass | Gravitational potential energy per unit mass |
| quantity | vector | scalar |
| equation |
towards the centre of the source mass |
|
| relationship to mass | Force, = mg | Potential energy, = mϕ |
| graph | 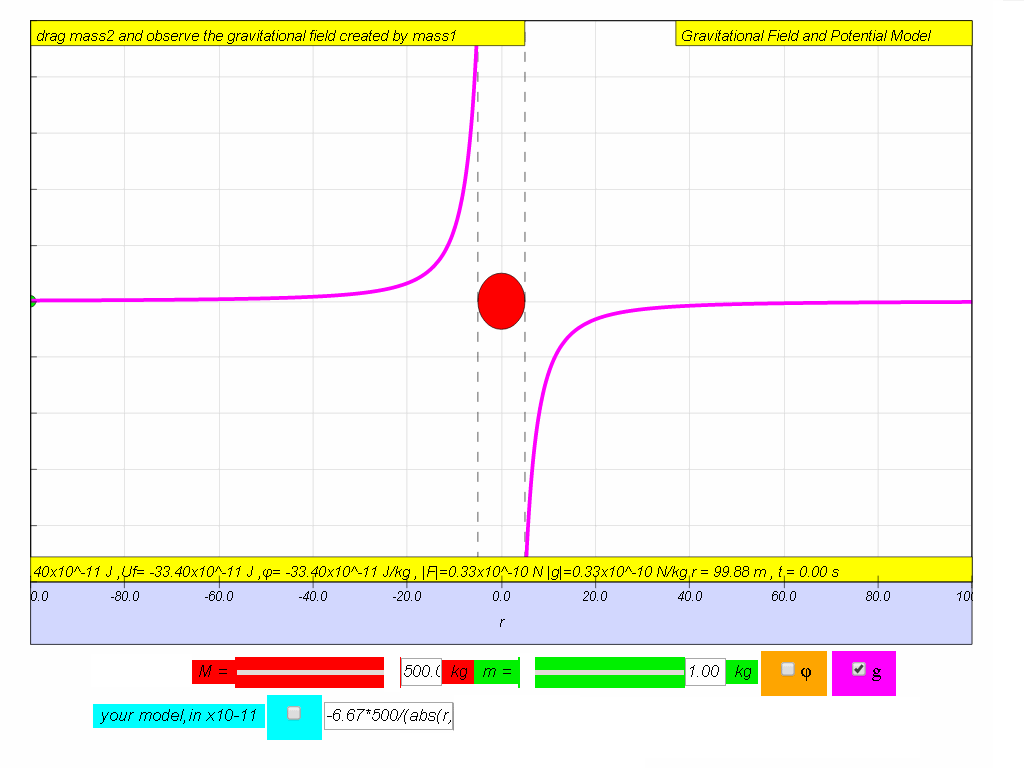 |
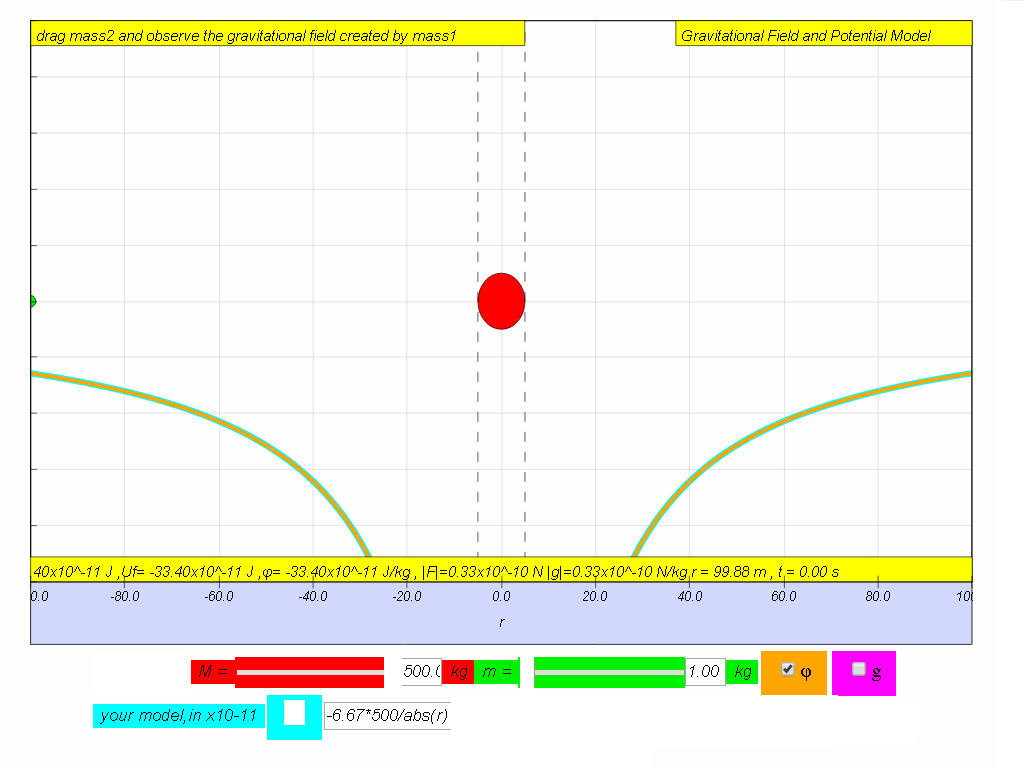 |
| computer model if M = 500. | -6.67*500/(abs(r)*r) | -6.67*500/abs(r) |
| relationship between g and ϕ |
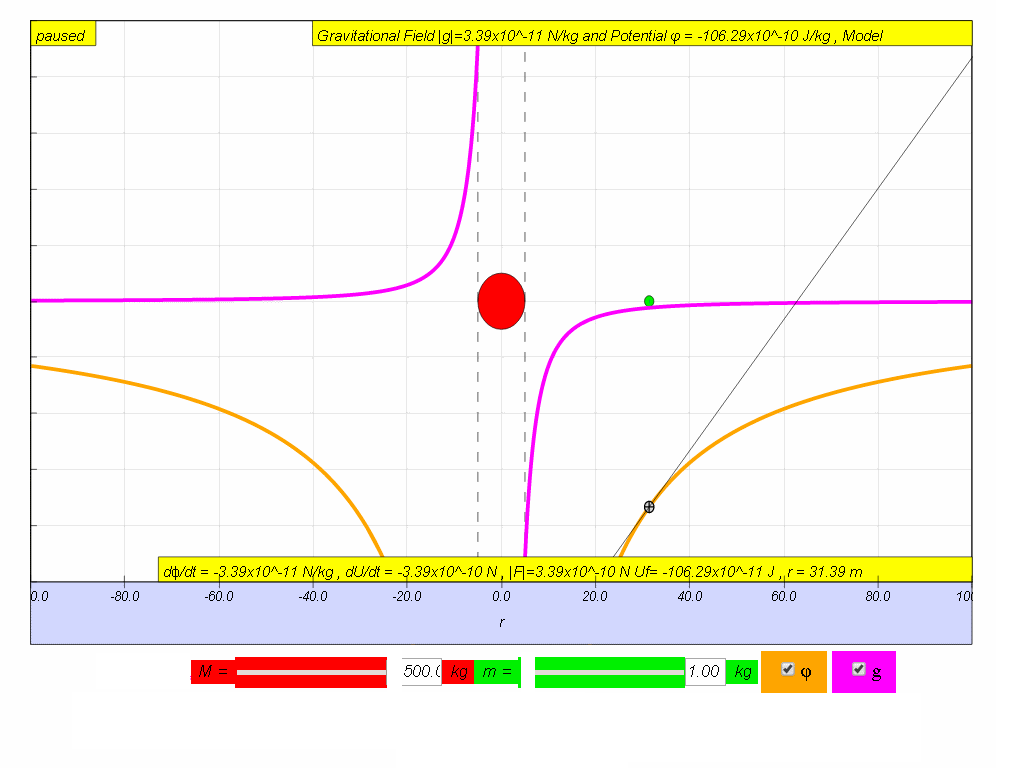 |
|
| relationship between F and U |
 |
|
7.3.8.3 Model
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


![]()
 This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre
This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre
Other Resources
- http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GField_and_Potential_1D_v8wee.jar
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 08 Gravity
- Hits: 7339