About
1.2.11 Example: Spring-mass system
A mass suspended from a spring, displaced vertically and released to move
freely to produce up and down motion
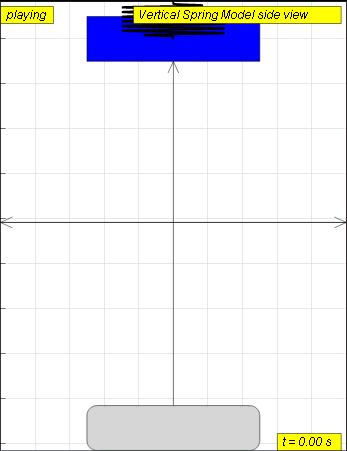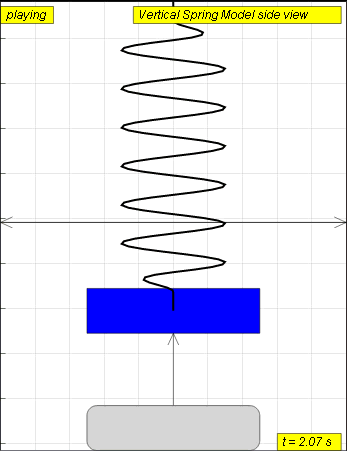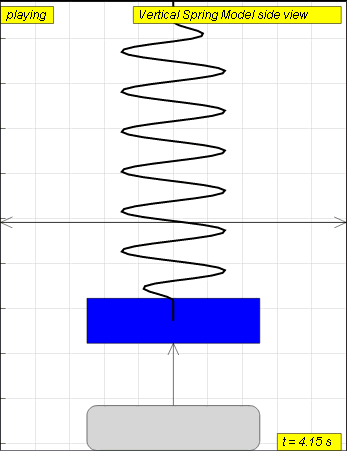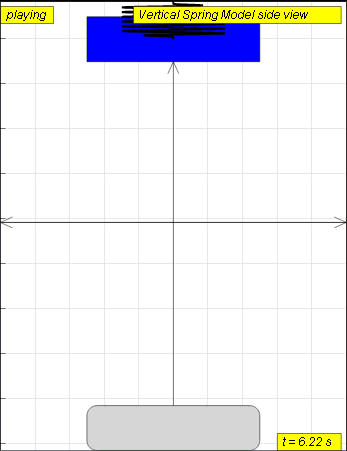
The model view of a mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion with right panel showing the displacement, velocity and acceleration.
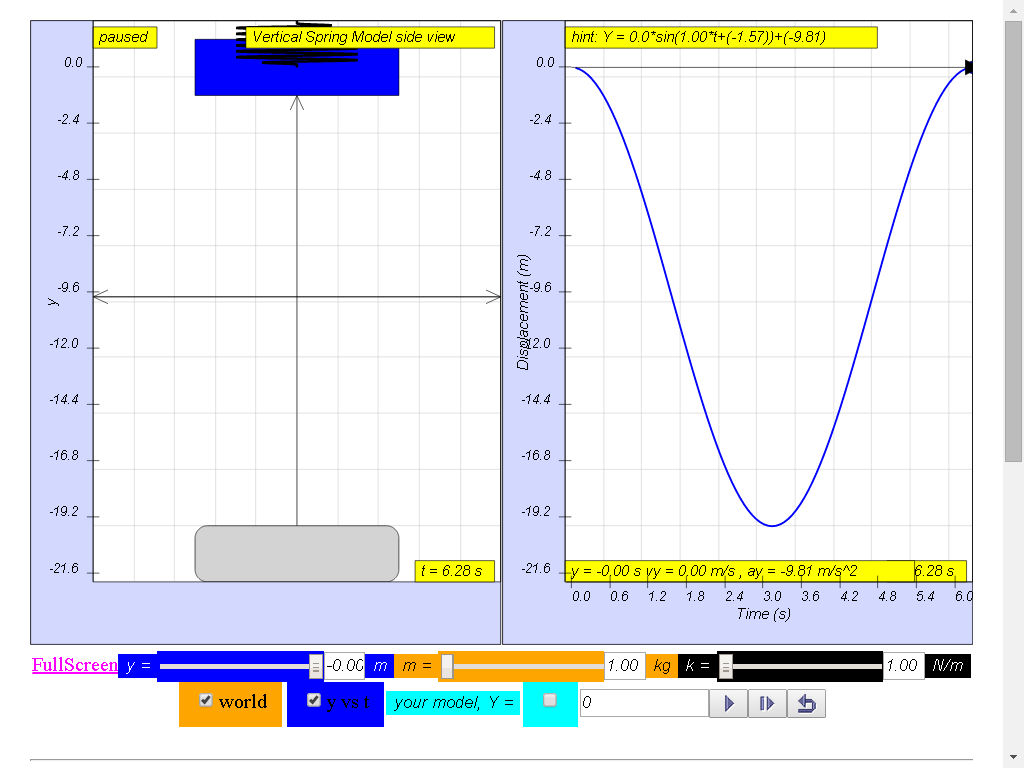
Q1: under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?
H1: the model assumes the restoring force by the spring is F = -ky, it is
always correct for any magnitude of oscillation y in real springs. Is it
always valid in the real spring motion when the spring is hyper extending
beyond the linear limits of Hooke's Law ?
Q2: change the simulation y=0 m and Play the model. In the your model Y = _________, suggest your own suitable model that can describe the motion y.
Q3: in this same motion, propose the velocity and acceleration model(s)
Q4: carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y0sin(ωt+φ)+Yshift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y0 , ω , φ , and Yshift.
Q5: similarly, suggest whether the model(s) for velocity, vY =ωY0cos(ωt+φ) and
aY = - ω2Y0sin(ωt+φ). Test them out using an example of your choice.
1.2.11.1 YouTube
http://youtu.be/P-Umre5Np_0 MIT Physics Demo -- Spray Paint Oscillator. A can of spray paint is attached to a spring oscillator. A roll of paper is run past the oscillating can. The result is a sine wave - http://en.wikipedia.org/wiki/Sine_wave - on the paper.Watch the original video on MIT TechTV - http://techtv.mit.edu/videos/803-spray-paint-oscillator1.2.11.2 Tracker activity:
http://weelookang.blogspot.sg/2012/08/tracker-modeling-in-spring-mass-system.html1.2.11.3 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Other Resources
Press the play button. Watch the graph to see how the height of the mass changes as it moves up and down. Use the graph to determine the period of the mass-spring system. Adjust the scale by dragging the numbers on the axes. Change each variable – gravity, spring constant, starting distance and mass – and observe how each one affects the period. Can you explain why? Is this different from the relationships for a pendulum? Try the damping slider. Does damping change the period?
Press the play button. Watch the graphs to see the motion of the spring pendulum. Can you distinguish the pattern of spring motion (up and down) from the pattern of pendulum motion (back and forth)? How are the two related? Is there a regular pattern to the motion? Compare the periods of the two graphs. How many different patterns can you produce by changing the variables – gravity, rod length, mass and spring constant? Under what conditions does the energy switch between back and forth and up and down? Does the initial starting angle affect the patterns when all the other variables are unchanged?
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Fremont
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 4361


.png
)





