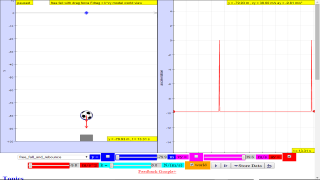
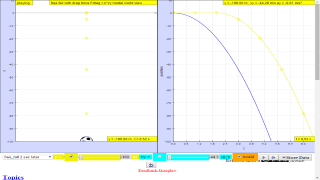
About
Topics
KinematicsSpeed, velocity and acceleration
Graphical analysis of motion
Free-fall
Effect of air resistance
Description
This simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged
(iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged
When only the velocity-time graph check-box is selected, it can be explored for the following cases too.
(ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t
(iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t
(iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes).
The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2.
Lastly, by selecting the 3 options of
"free fall"
"free_fall_with_small_air_resistance"
"free_fall_with_large_air_resistance"
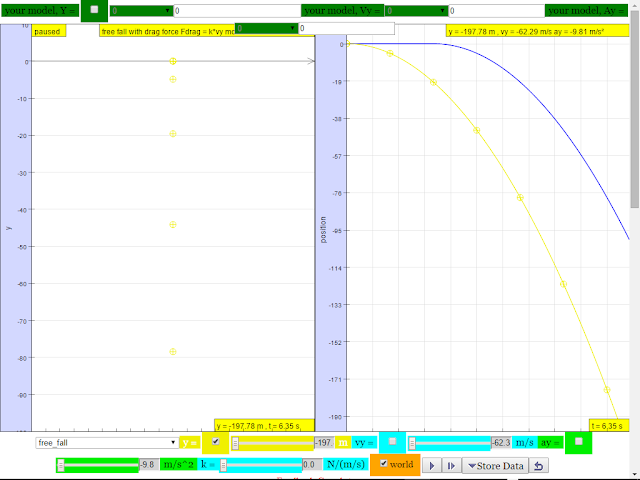
It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration.
Sample Learning Goals
(f) deduce from the shape of a displacement-time graph when a body is:
(ii) moving with uniform velocity
(iii) moving with non-uniform velocity
(g) deduce from the shape of a velocity-time graph when a body is:
(ii) moving with uniform velocity
(iii) moving with uniform acceleration
(iv) moving with non-uniform acceleration
(i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2
(j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity
Version:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


 This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Félix J. García
This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Félix J. García
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.freefallapp633230

https://itunes.apple.com/us/app/free-fall-simulator-ios/id1198493068?ls=1&mt=8
Worksheet
- ejss_model_kinematics CT_kinematics (1017).ppt 2017 by Dave
- ejss_model_kinematics Motion in One Dimension student worksheet (2017).docx 2017 by Dave
- Motion in One Dimension student worksheet (dl-gwf) Link1, Link2 by Lyna, Gavin, Dave and lookang
Examples
From Dave and Gavin,
1.A sky diver jumps out of a hovering helicopter. A 2 seconds afterwards another sky diver jumps out and they both fall along the same vertical line. Ignore air resistance so that both sky divers fall with the same acceleration.
a.Does the difference in their speeds stay the same throughout the fall?
 |
| https://iwant2study.org/ospsgx/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: after t =2 s, the difference is always the same difference as shown by the constant difference.
b.Does the vertical distance between them stay the same throughout the fall?
 |
| https://iwant2study.org/ospsgx/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: after t =2 s, the difference in position increases as shown by the increasing difference of YELLOW minus BLUE line.
Question 2
2.A tennis ball thrown from the top of a building is given an initial velocity of 20 m/s straight upward. The building is 50 m high, and the ball just misses the edge of the roof on its way down. Using t = 0 as the time the ball leaves the thrower’s hand, determine
a.the time at which the ball reaches its maximum height
 |
| https://iwant2study.org/ospsgx/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: t = 2.0 s
b.the maximum height
suggested answer: H maximum = 70.4 m
c.the time at which the ball returns to the height from which it was thrown
 |
| https://iwant2study.org/ospsgx/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: t = 4.0 or 4.1 s
d.the velocity of the ball at this instant
suggested answer: v = -20.2 m/s
e.the velocity and position of the ball at t = 5 s
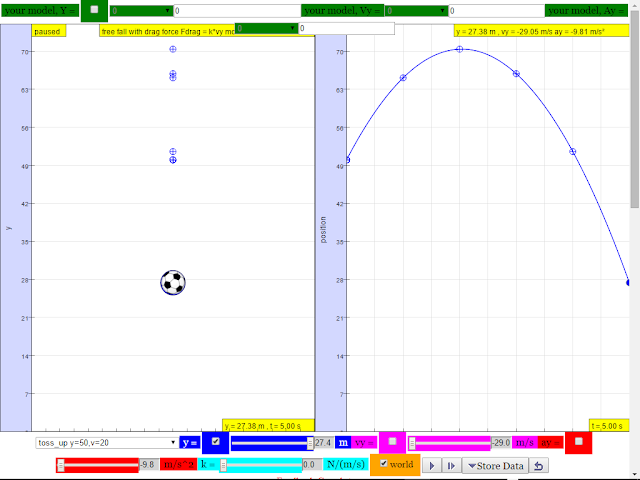 |
| https://iwant2study.org/ospsgx/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
Key inquiry question:
How can we describe the motion of objects moving in a straight line?
1. Speed, velocity and acceleration
• Physical quantities can be scalar (e.g. distance, speed) or vector (e.g. displacement, velocity, acceleration) quantities. Scalar quantities can be added algebraically. Vector quantities can be added using graphical methods (parallelogram method or ‘head-to-tail’ method).
• Average speed of a body is given by total distance travelled / total time taken (v = d/t). Instantaneous speed is the speed at any instant.
• Acceleration of a body is defined as its change in velocity / time taken (a = (v - u)/t). The direction of acceleration is the direction of the change in velocity.
• Acceleration is: zero when velocity is constant (i.e. no change in velocity); positive (object is accelerating) when velocity is increasing; negative (object is decelerating) when velocity is decreasing
2. Graphical analysis of motion
• Displacement-time and velocity-time graphs of a body allow us to deduce when the body is: at rest; moving with uniform velocity and acceleration; moving with non-uniform velocity and acceleration.
• Gradient of a displacement-time graph gives the velocity of the moving object; Gradient of a velocitytime graph gives the acceleration of the moving object; Area under a velocity-time graph gives the displacement travelled by a body.
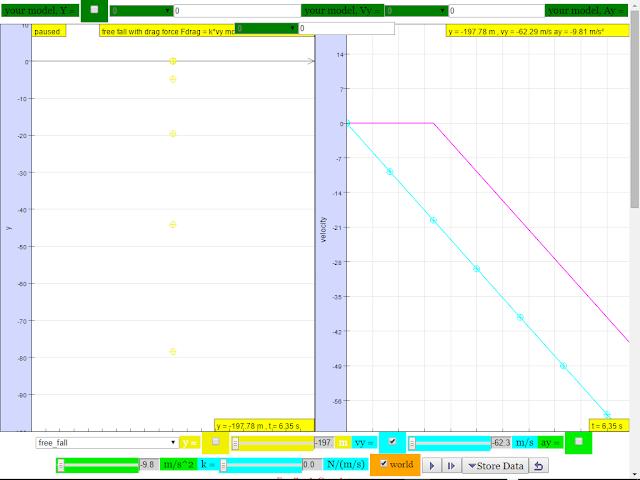
3. Free fall
• An object is in free fall if the only force acting on it is the force of gravity (it’s weight), i.e. no air resistance or contact forces act on the falling object.
• Acceleration of free fall, g for a body near to the Earth is constant and is approximately 10 m/s2 (regardless of the object’s mass or size).
4. Effect of air resistance
• The motion of bodies with constant weight falling with or without air resistance are different (without air resistance, object will have constant acceleration and velocity increases continuously; with air resistance, velocity reaches maximum value or terminal velocity when the force due to air resistance = weight, and acceleration becomes zero). Terminal velocity occurs only when air resistance is considered
Students’ prior knowledge of Kinematics
Primary level:
Students will not have been introduced to the concepts to describe motion. They would have knowledge of the effects of a force to stop or move an object; change its speed (move faster or slower) or direction of motion.
Lower secondary level:
Students learn that speed:
• is a measure of how fast an object is moving;
• depends on the distance (length) travelled and the time taken (unit: m/s).
Objects usually do not move at the same speed, hence, it is more useful to measure its average speed which is defined as total distance travelled / total time taken. Speed at any instant is the average speed over an extremely short time interval.
Students’ common misconceptions and learning difficulties in Kinematics
Displacement, velocity and acceleration:
- Students’ concepts of displacement, velocity, and acceleration are not well differentiated.
- They often think that: same position means same velocity for two objects; same velocity means same acceleration for two objects; larger (or smaller) velocity means larger (or smaller) acceleration; zero velocity means zero acceleration; and acceleration and velocity are always in the same direction.
- Displacement-time and velocity-time graphs: Students often view the position and velocity graphs as the actual path of the object, rather than a graphical representation of an object’s motion
- A hammer will reach the bottom (Moon’s surface) first as it is heavier than the feather since there is higher gravitational pull on the hammer, when in fact the hammer and feather have the same acceleration due to gravity and they will reach the ground at the same instance in an environment where there is no air resistance.
- Some students treat gravitational force and weight as separate forces, when in fact Weight of an object is the gravitational force between the object and the Earth.
- Students think that an external force is necessary to keep an object in motion when in fact An object does not need an external force to keep it moving at a constant speed in a straight path, if forces opposing motion such as friction is negligible.
Computational Thinking
-
Students observe the motion of a bouncing ball and are challenged to describe its motion.
-
Students take a video of the actual motion of the bouncing ball (concrete representation) and analyse its motion using more abstract representations such as motion diagrams and graphs, with the aid of the Tracker software (see Fig. 1 and Fig. 2)).
-
Students explain the motion of the bouncing ball by drawing conceptual links between motion, force (with the aid of free- body diagrams) and energy.
Extension: students use a computer simulation ( http://iwant2study.org/lookangejss/02_newtonianmechanic s_2kinematics/ejss_model_freefall01/freefall01_Simulation. xhtml ) to consolidate, apply and extend their learning for different scenarios, with particular focus on the mathematical representation of motion (e.g. modelling motion with and without air resistance).
-
Computational thinking data practices (e.g. collecting, manipulating, analysing and visualising/representing data) and modelling motion of objects mathematically
-
Students experience translating a physical phenomenon in its concrete representation (i.e. data in the form of actual videos of moving objects) to more abstract graphical forms. They learn the importance of calibration, choice of reference point and explicating data frame-by-frame that allows for valid and useful analysis. In doing so, students better understand how the various representations relate to kinematics concepts (e.g. displacement, velocity and acceleration).
-
Students learn to interpret the given representations and to translate between different representations, and to assess the strengths and weaknesses of different representations.
Versions
- http://weelookang.blogspot.sg/2016/01/ejss-free-fall-simulation-added-more.html Blogpost on more cases added
- http://weelookang.blogspot.sg/2014/03/ejss-kinematics-in-y-model.html Blogpost on JavaScript version by Loo Kang Wee
- http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.html Blogpost on JavaScript version by Loo Kang Wee
- http://weelookang.blogspot.sg/2013/12/ejss-kinematics-model.html template objects from lookang
- http://weelookang.blogspot.sg/2010/09/ejs-open-source-bouncing-ball-with-drag.html Blogpost on Java vesion by Loo Kang Wee and Fu-Kwun Hwang
- http://weelookang.blogspot.sg/2010/06/ejs-open-source-kinematics-java-applet.html
- http://www.compadre.org/osp/items/detail.cfm?ID=13050 Physlet One-Dimensional Kinematics Illustrations Package by Andreu Glasmann, Wolfgang Christian, and Mario Belloni
Other Resources
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=421.0 Elastic bouncing ball Java Version by Fu-Kwun Hwang
- http://butikov.faculty.ifmo.ru/Projects/Falling_bodies.html#_applet Falling Object Java 3D version by Eugene Butikov
- https://www.geogebra.org/m/rfmnbhev by seng kwang
- https://www.geogebra.org/m/dfb53dps by seng kwang
Other Hands-on kit
- https://sites.google.com/site/iprofmeca/session-1-free-fall by This email address is being protected from spambots. You need JavaScript enabled to view it.
Project related:
- AEP 03/16 LW Apps as Virtual Lab
- Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction Project Number: OER 10/15 GWF Project Duration: 01 July 2015 - 30 April 2017 http://weelookang.blogspot.sg/2015/07/understanding-teacher-learning.html
Family of Resources
| Secondary | Primary | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion Free-fall Effect of air resistance DescriptionThis simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t (iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes). The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2. Lastly, by selecting the 3 options of "free fall" "free_fall_with_small_air_resistance" "free_fall_with_large_air_resistance" It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration. Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (ii) moving with uniform velocity (iii) moving with non-uniform velocity (g) deduce from the shape of a velocity-time graph when a body is: (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2 (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity Version:ball taken from: http://psychology.wikia.com/wiki/File:Soccer_ball.svg http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.htmlFor Teachers
Teacher-Submitted Activities
Share an activity! email Translations
Software Requirements
Credits
|
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion Free-fall Effect of air resistance DescriptionThis simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t (iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes). The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2. Lastly, by selecting the 3 options of "free fall" "free_fall_with_small_air_resistance" "free_fall_with_large_air_resistance" It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration. Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (ii) moving with uniform velocity (iii) moving with non-uniform velocity (g) deduce from the shape of a velocity-time graph when a body is: (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2 (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity Version:ball taken from: http://psychology.wikia.com/wiki/File:Soccer_ball.svg http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.htmlFor Teachers
Teacher-Submitted Activities
Share an activity! email Translations
Software Requirements
Credits
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}- Details
- Parent Category: 03 Motion & Forces
- Category: 01 Kinematics
- Hits: 32551


.png
)