About
1.2.8 Example
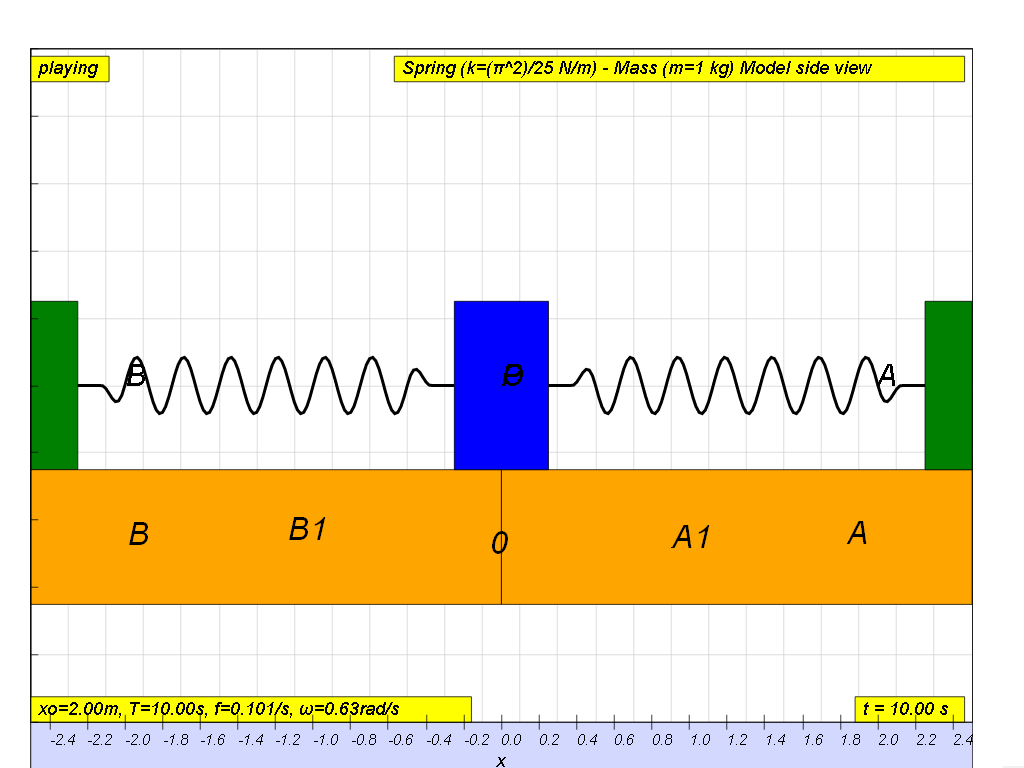
A particle moves in a simple harmonic motion between O to A and B and back to O as shown. The positions B, B1, O, A1 and A are equally spaced. The time taken to travel from A to B is 5.00 s and the distance AB is 4.00 m.
a) Write an equation to represent the given simple harmonic motion.
b) During one cycle, find the time that the particle stays in the region:
i) A-A1
ii) A1-B1
[ x = 0.200 sin (0.628 t) , 0.833 s , 3.33 s ]
Hint:
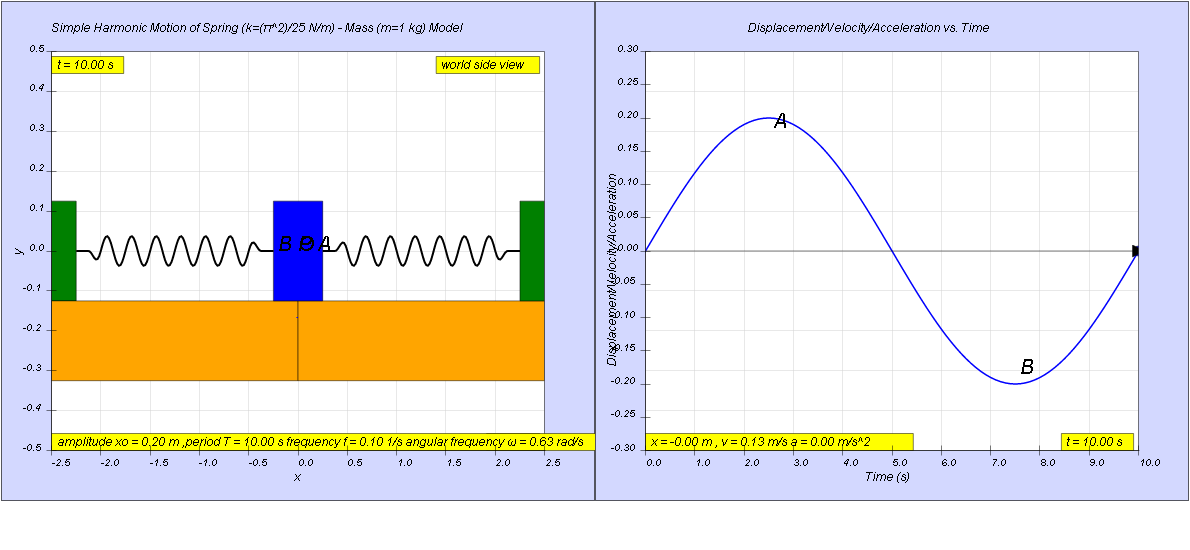
1.2.8.1 Solution:
a) since x0 is half of AB = 4 m
x0 = 2.00 m
the equation is x = x0 sin(ωt)
to find ω, and we can given T, we use
thus the equation is x = 2.00 sin(0.628t)
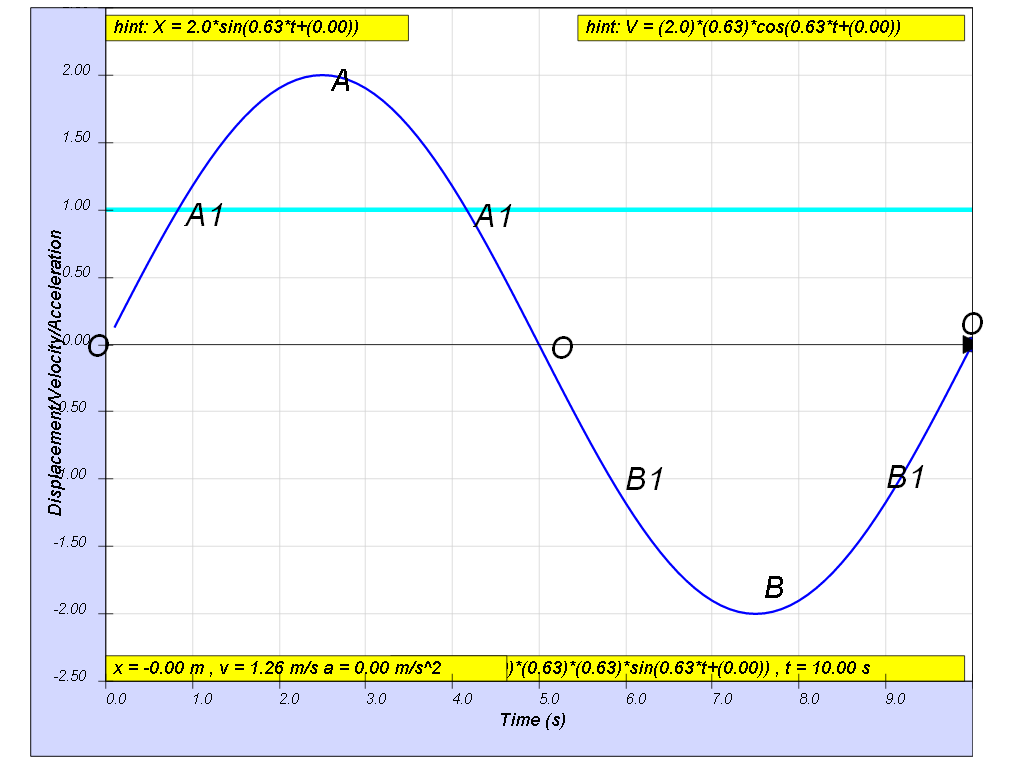
b) the strategy is to find the time which all the points B, B1, O, A1 and A occurs.
to find time from A to A1,
when x = A1 = 1.00, imply 1.00 = 2.00 sin (0.628t), therefore tA1 = 0.833 s
similarly, when x = A = 2.00, imply 2.00 = 2.00sin (0.628t), therefore tA = 2.50 s
time from A1 to A = tA -tA1 = 2.50 - 0.833 = 1.66 s
therefore time from A1 to A to A1 = (1.66)(2) = 3.33 s
b) since we know t 0 to A1 = 0.833 s
by comparing the 4 equal sections of OA1 = A1O = OB1 = B1O = 0.833 s
the total time spent inside A1B1 = (4)(0.833) = 3.33 s
1.2.8.2 Model
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.