About
Topics
Light
Refraction of light
Modeling for Snell's Law
In this Fermat Principle Model, the simulation shows the light path in the least possible time.
(d) recall and apply the relationship sin i / sin r = constant to new situations or to solve related problems
(e) define refractive index of a medium in terms of the ratio of speed of light in vacuum and in the medium
Modeling for Snell's Law
Description
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light.In this Fermat Principle Model, the simulation shows the light path in the least possible time.
Sample Learning Goals
(c) recall and use the terms for refraction, including normal, angle of incidence and angle of refraction(d) recall and apply the relationship sin i / sin r = constant to new situations or to solve related problems
(e) define refractive index of a medium in terms of the ratio of speed of light in vacuum and in the medium
Activities
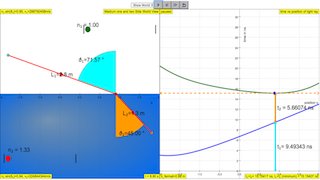
- Select the (drag and release the dots) desired position 1 and 2 of which light ray (RED) must be transmitted and received.
- Click run and the simulation will make the point of ray with the medium 1 and 2 interface, move and compute the following assuming point 1 (start TEAL color) and point 2 (end ORANGE color)
- L1=Math.sqrt((xc-x1)*(xc-x1)+(yc-y1)*(yc-y1))
- L2=Math.sqrt((xc-x2)*(xc-x2)+(yc-y2)*(yc-y2))
- time taken in medium 1, t1=n1*L1/c where n1 is refractive index of medium 1, c is speed of light
- time taken in medium 1, t2=n2*L2/c; where n2 is refractive index of medium
- using the evidences of t1 + t2 graph of ( time vs position x) , suggests what is the path that has the smallest travelling time, in other words the meaning of t1 + t2 is a minimum?
- using Snell's Law, verify if Fermat's principle is agreeable to Snell's Law?
- Calculate the error in the Snell's Law, n₁ sin(ϑ₁)=n₂ sin(ϑ₂) and Fermat's principle.
- Suggest a reason why the 2 answers are not exactly identical.
Version:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


Fu-Kwun Hwang; lookang; tina
end faq
Versions
- http://weelookang.blogspot.sg/2015/07/ejss-fermats-principle-refraction-model.html JavaScript version of Fermat's principle by Fu-Kwun Hwang and Loo Kang Wee
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2494.0 Java version of Fermat's principle by Fu-Kwun Hwang
Other Resources
Facebook Social Comments